백준 3012 / 올바른 괄호 문자열 / DP, 분할 탐색 / JAVA / 플레티넘 3
오늘은 백준 3012번 <올바른 괄호 문자열> 문제를 풀어보려고 한다. 이 문제는 07/08 크로아티아 정보올림피아드 기출문제이다.
https://www.acmicpc.net/problem/3012
3012번: 올바른 괄호 문자열
예제 1의 경우 다음이 가능하다. ({([()])}), ()([()]{}), ([([])]{})
www.acmicpc.net
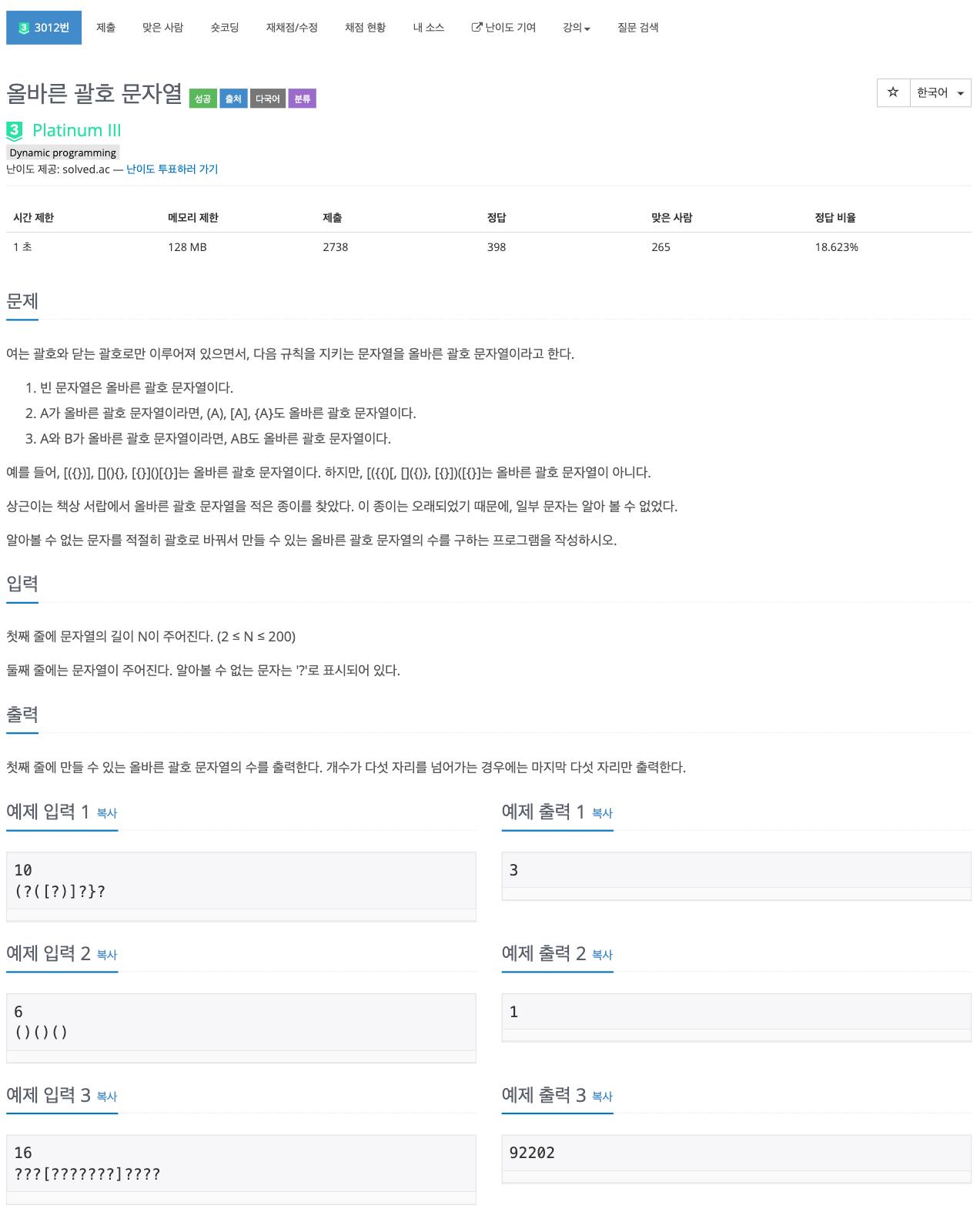
크로아티아 정보올림피아드 기출 문제여서 그런지 문제에 대한 아이디어가 쉽게 떠오르지는 않았던 것 같다. (난이도도 심지어 플레티넘 3 ㄷㄷ...) 처음에는 ? 각각에 들어갈 수 있는 문자 "{", "[", "(" 등을 찾아서 경우의 수를 생각해 주어야 하나? 라고도 떠올려 봤는데 너무 생각해 주어야 할 케이스가 많았고 이 방법은 맞지 않다는 것을 깨달았다. 결국 DP를 통해 한 번 계산한 연산은 메모이제이션을 통해 다시 연산하지 않으면서 성능을 끌어올려서 N이 큰 값이 들어와도 시간 내에 계산을 할 수 있는 방법이 최적의 방법이라는 결론에 도달하게 되었다.
문자열의 길이가 N이라면 시작 인덱스를 0, 끝 인덱스를 N-1으로 설정해서 탐색을 시작한다. 그리고 시작 인덱스 s 에서 끝 인덱스 e까지 만들 수 있는 올바른 괄호 문자열의 갯수를 dp[s][e]에 넣는다. 그리고 dp[s][e]를 구해서 10만 이하의 값이면 그대로, 10만 이상의 값이면 마지막 다섯 자리만 출력해 주면 정답이 되는 것이다. 그리고 dp에 시작 인덱스부터 끝 인덱스까지의 올바른 괄호 문자열의 갯수를 구한 값은 한 번 연산을 하면 다시 할 필요 없도록 가져와 쓸 수 있게 boolean 타입 check[][] 배열을 하나 더 만들어서 중복 연산을 피해 주기로 했다.
long solve(int s, int e) 라는 메서드가 바로 dp[s][e]를 구하는 메서드이다. 문자열의 길이가 N인 경우 solve(0, N-1)을 실행한다. 이 안에서 만약 s>e 인 경우는 연산을 수행할 수 없으므로 return 1을 해주고 이미 한 번 연산이 된 경우라면(check[s][e] = true) 해당 범위 문자열 갯수 값인 dp[s][e]를 리턴해준다.
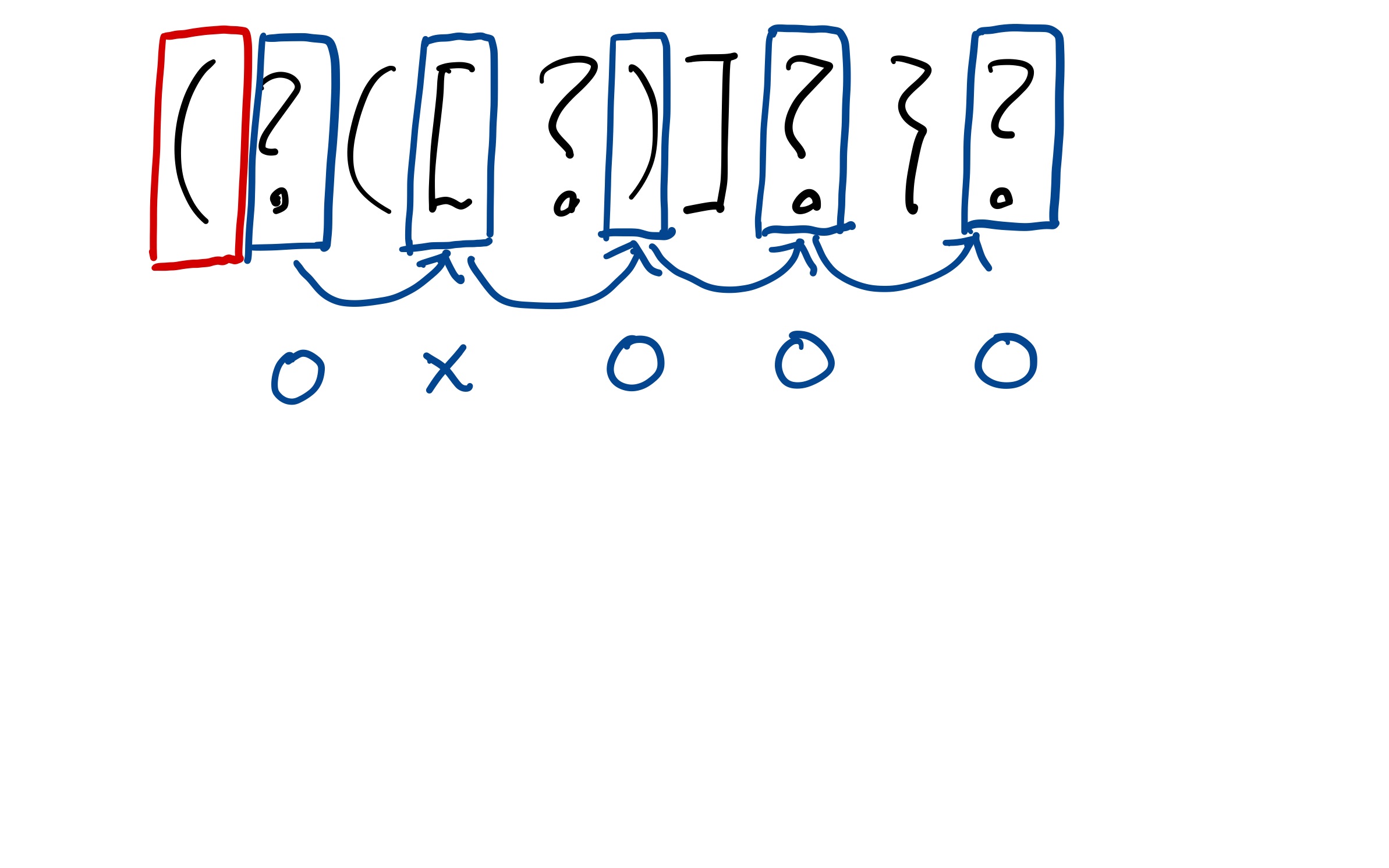
그림에서 보이는 것처럼 가장 왼쪽 괄호부터 순차적으로 탐색을 시작한다. 여기서 주의해야 할 점이 탐색을 할 때 모든 문자열을 탐색하는 것이 아니라, 인덱스를 2씩 건너서 계산한다. 그 이유는 분할을 해서 올바른 괄호 문자열을 만들어 주어야 하는데 그러기 위해서는 각각의 덩어리가 짝수가 되어야 하기 때문이다. 그리고 체크를 하면서 빨간색으로 표시한 '('로 열고, ')'으로 닫아줄 수 있는 경우(위의 예시에서는 1,3,4,5번째)만 체크해서 연산을 수행한다. 만약 여는 괄호와 닫는 괄호가 짝이 맞지 않는다면 올바른 괄호 문자열이 될 수 없기 때문에 굳이 연산을 수행해 줄 필요가 없다.
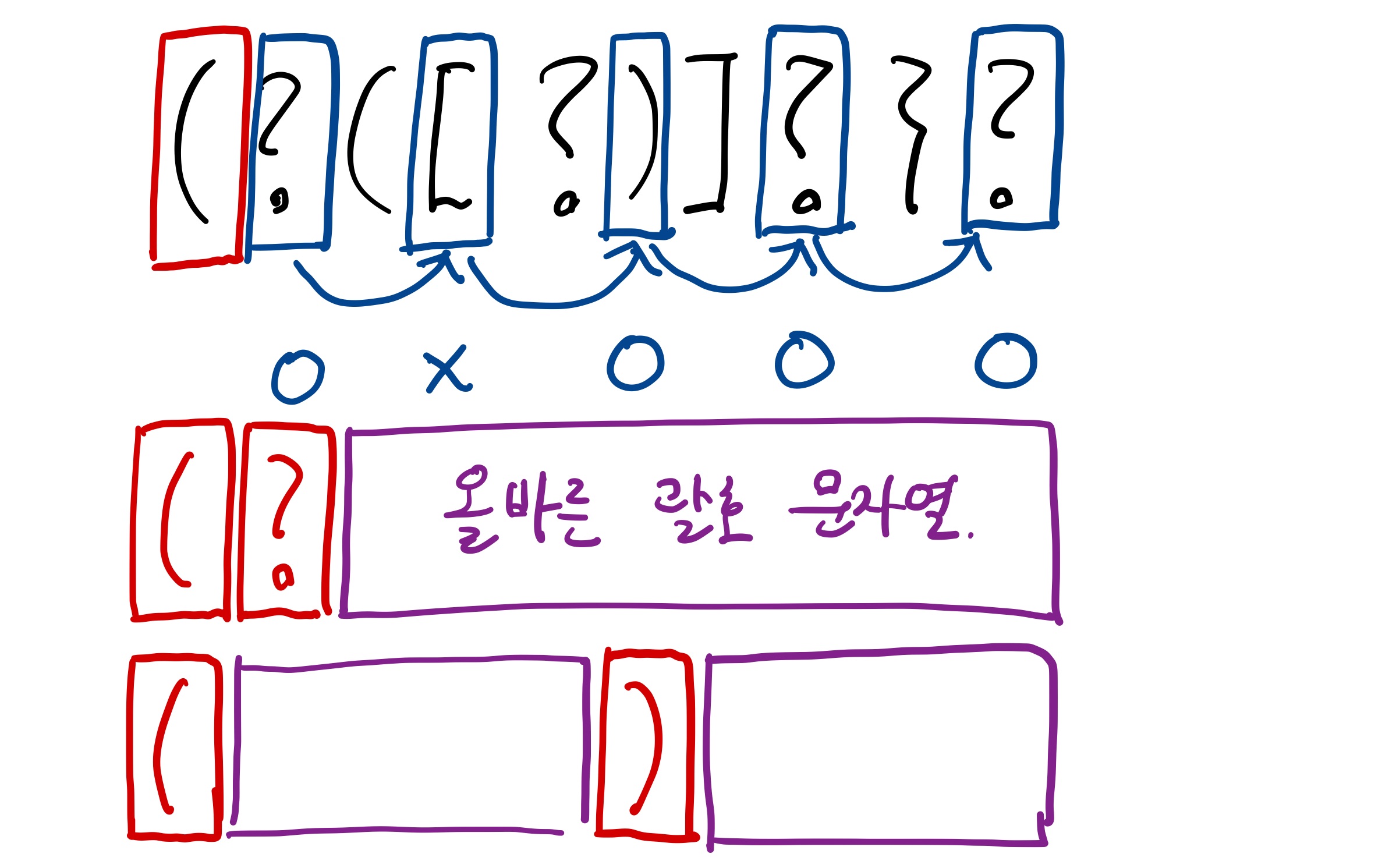
이 예제의 경우 첫 번째 빨간색 '(' 여는 괄호에 대해서는 1,3,4,5 번째 닫는 괄호를 체크해 준다. 1번째 닫는 괄호는 '?'인데 여기에는 ')'가 들어가야 할 것이고, 나머지 보라색 부분이 올바른 괄호 문자열이 되면 이 전체 길이 N인 문자열은 올바른 괄호 문자열이 된다. 따라서 여는 괄호의 인덱스를 s, 닫는 괄호의 인덱스를 k라고 하면 [s ... k] [k+1 ... e] 이렇게 두 덩이의 올바른 괄호 문자열로 나뉘어질 수 있는지를 체크하고 그렇다면 가능한 문자열의 갯수를 모두 더해서 dp[s][e]에 더해준다. 3번째 닫는 괄호의 경우 '('와 ')'사이의 문자열이 올바른 괄호 문자열인지, 그리고 그 오른쪽도 올바른 괄호 문자열인지를 체크해서 각각의 경우의 수를 곱해준 후 dp[s][e]에 더해주면 된다.
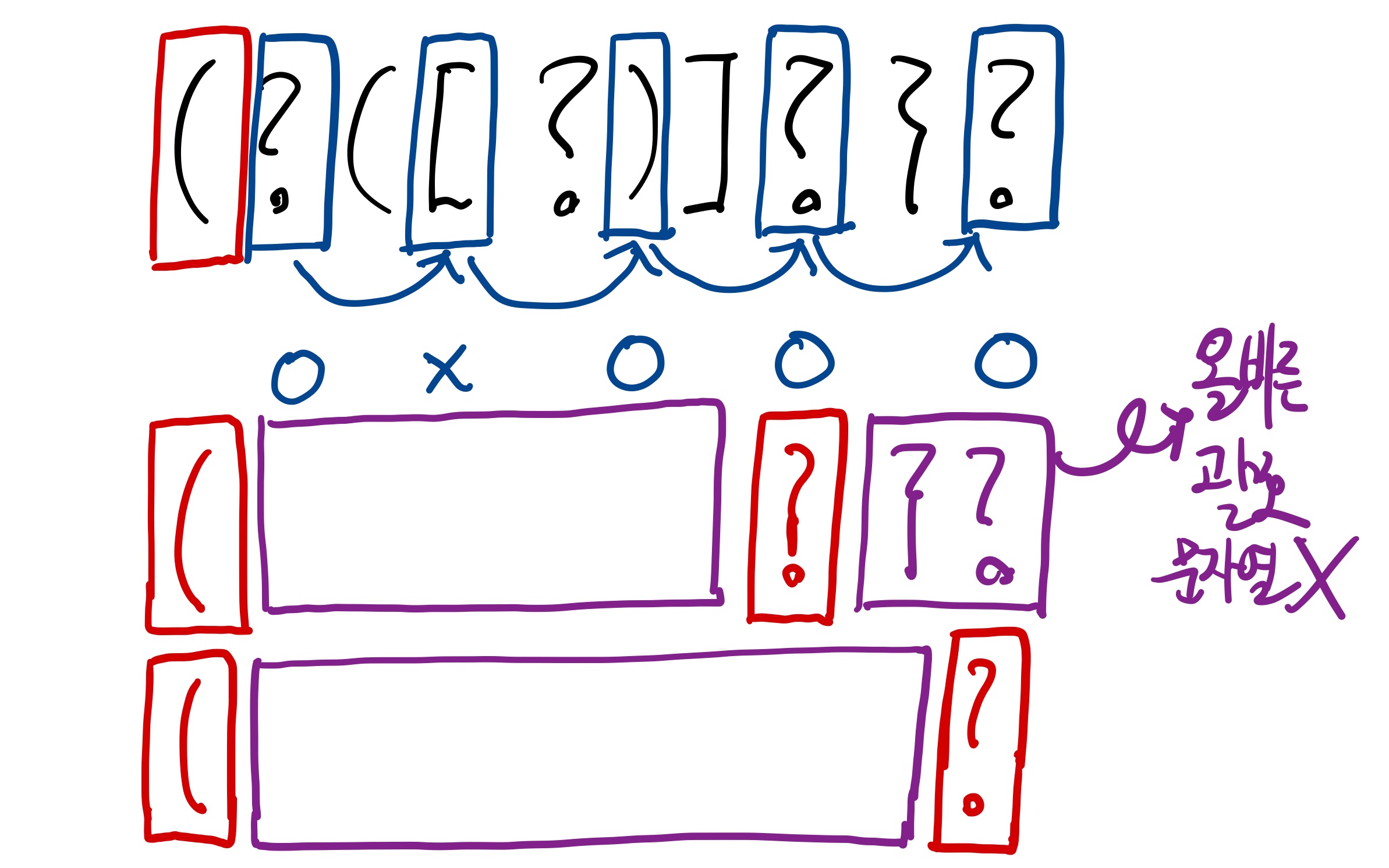
4번째 닫는 괄호의 경우 오른쪽의 문자열이 '}', '?' 으로 이루어져 있는데, 이는 올바른 괄호 문자열이 될 수 없다. 따라서 이 경우는 올바른 괄호 문자열이 발생할 가능성이 없다. 5번째 닫는 괄호의 경우는 '('와 '?' 사이의 문자열이 올바른 괄호 문자열이 되는지만 체크해 주면 되므로 solve(s+1, k-1)을 구해서 dp[s][e]에 더해주면 될 것이다.
이런식으로 발생할 수 있는 모든 가능성을 전부 더해준 후 그냥 결과를 출력하면 틀린다. 문제에서 10만 이상의 수가 나올경우 마지막 다섯 자리만 출력하라고 하였기 때문이다. 만약 답이 303이 나오면 그냥 303을 출력하면 되는데 1000303이 나오면 00303을 출력해야 하는 것이다. 이렇게 결과가 10만 이상인지 아닌지에 따라서 다르게 처리를 해준 후 출력을 하면 문제를 맞힐 수 있게 된다.

이 문제에 대한 내 자바 풀이는 다음과 같다.
그리고 문제출제 기관에서 발표한 C++로 짜여진 정답 소스코드도 같이 첨부한다.
플레티넘이라 쉽지 않은 문제이다. 하지만 DP의 개념을 응용해 보기 좋은 문제이고, Edge case에 대한 고민도 해볼 수 있어서 실력을 쌓는데는 큰 도움이 될 수 있을 것 같다!