카카오 19겨울인턴 4번 / 유니온 파인드(Union Find) / JAVA
오늘 살펴볼 문제는 카카오 19년 겨울인턴 코딩테스트 4번 <호텔 방 배정> 문제이다.
https://programmers.co.kr/learn/courses/30/lessons/64063
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr

카카오는 매번 코딩테스트마다 문제 해설을 자사 블로그에 공개한다. 관심있는 분들은 읽어 보아도 좋을 것 같다.
2019 카카오 개발자 겨울 인턴십 코딩 테스트 문제 해설
2019 카카오 개발자 겨울 인턴십 코딩 테스트 문제 해설 – tech.kakao.com
“2019년 카카오 개발자 겨울 인턴십” 공개 채용을 위한 1차 코딩 테스트가 지난 2019년 11월 9일 오후 2시부터 6시까지 총 4시간에 걸쳐 진행되었습니다. ’19년 신입공채 1차 코딩 테스트 시에 7문�
tech.kakao.com
호텔 방 배정 문제는 정확성과 효율성을 둘 다 갖춰서 풀어야 하는 문제 중 하나이다. 그렇기 때문에 단순하게 구현만 해서 맞는 것이 아니고 주어진 조건에 따라 시간복잡도까지 계산을 해서 맞추어야 한다. 이 문제도 마찬가지로, 단순하게 모든 방을 하나씩 탐색해서 풀게 될 경우 O(N^2)이라는 시간복잡도가 나오게 되는데 그러면 N = 200,000 이므로 시간초과가 나게 된다.
나는 이 문제를 유니온 파인드(Union Find)를 가지고 풀어보았다. 유니온 파인드에 대해서 먼저 간단하게 설명을 하고 문제를 보도록 한다.
유니온 파인드는 그래프 알고리즘의 일종으로, 다른 말로 서로소 집합(Disjoint Set)이라고도 한다. 여러 개의 노드가 존재할 때 노드들을 연결하여 같은 집합으로 묶어주고 이러한 특성을 이용할 때 많이 사용하게 된다.
유니온 파인드는 부모 노드 하나씩 타고 올라가 루트 노드를 찾아 나가는 find() 함수와 두 개의 트리를 합치는 union() 함수로 이루어져 있다. 이 문제에서는 해당 함수를 구현하는 부분까지는 묻지 않았지만 개념적으로는 알고 있으면 도움이 된다.
그러면 본격적으로 문제를 풀어보자.
고객이 원하는 방 번호를 순서대로 받는다.(room_number 배열) 만약에 해당 방이 비어있으면 그 방에 그대로 넣어 주면 되고, 비어있지 않으면 요청한 방번호 보다 큰 숫자들 중에 비어있는 가장 작은 번호의 방을 부여하는 식이다. 만약에 첫 고객이 2번 방을 요청하면 2번 방을 배정하고 두 번째 고객이 마찬가지로 2번 방을 요청하면 3번 방을 주는 식으로 방 배정을 해야 한다.
나는 여기서 Map 자료구조를 사용해 보았다. X번 방을 처음 요청한 사람이 있을 경우 Map에 key: X, value: X+1을 입력하는 것이다. 그러면 그 다음에 X번 방을 요청하는 사람이 나타났을 때 Map에서 key 값을 통해 X+1번 방을 바로 배정해 줄 수가 있다. 즉, key 번째 방을 요청했을 때 고객에게 배정하는 방이 value 번째 방이 되는 것이다. 이렇게 하면 매번 고객을 배정할 때 마다 모든 방을 일일이 탐색할 필요가 없게 된다.
문제에서 주어진 예제를 가지고 보자.
처음 세 명의 고객은 각각 1반, 3번, 4번 방을 요청했다. 모두 요청할 당시에 비어 있는 방이었으므로 그냥 바로 배정이 가능하다. 그리고 위에서 살펴본 것 처럼 value 값을 (key 값 + 1) 으로 설정하면 다음과 같이 Map에 데이터를 저장할 수 있다.
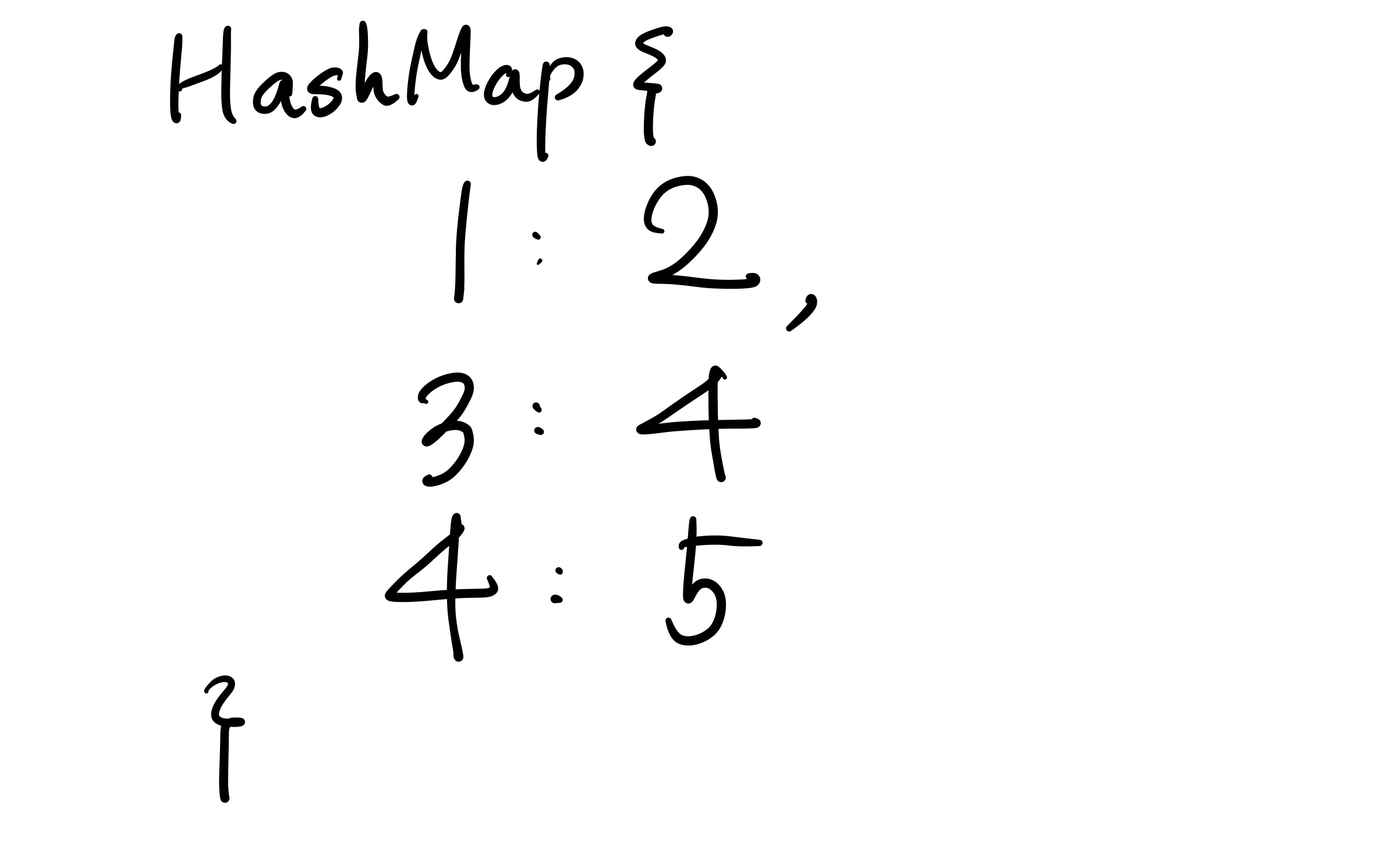
이를 트리로 하나씩 보면 다음과 같다. 먼저 첫 번째 고객이 1번 방을 요청했을 때이다.
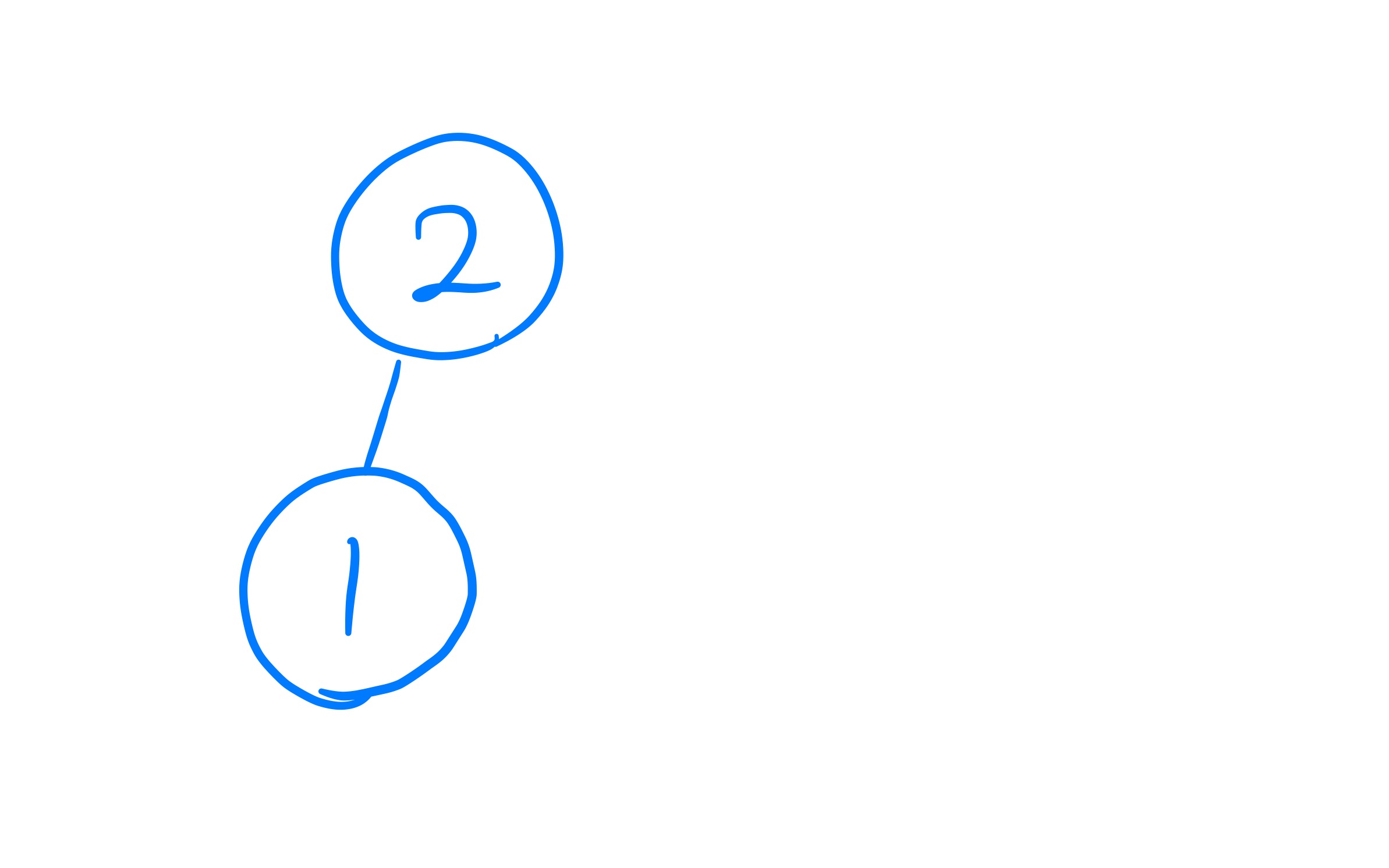
두 번째 고객이 3번 방을 요청했을 때이다.

세 번째 고객은 4번 방을 요청했다. 그런데 이미 4번 노드가 그림에 있으므로 이어서 그려보자.
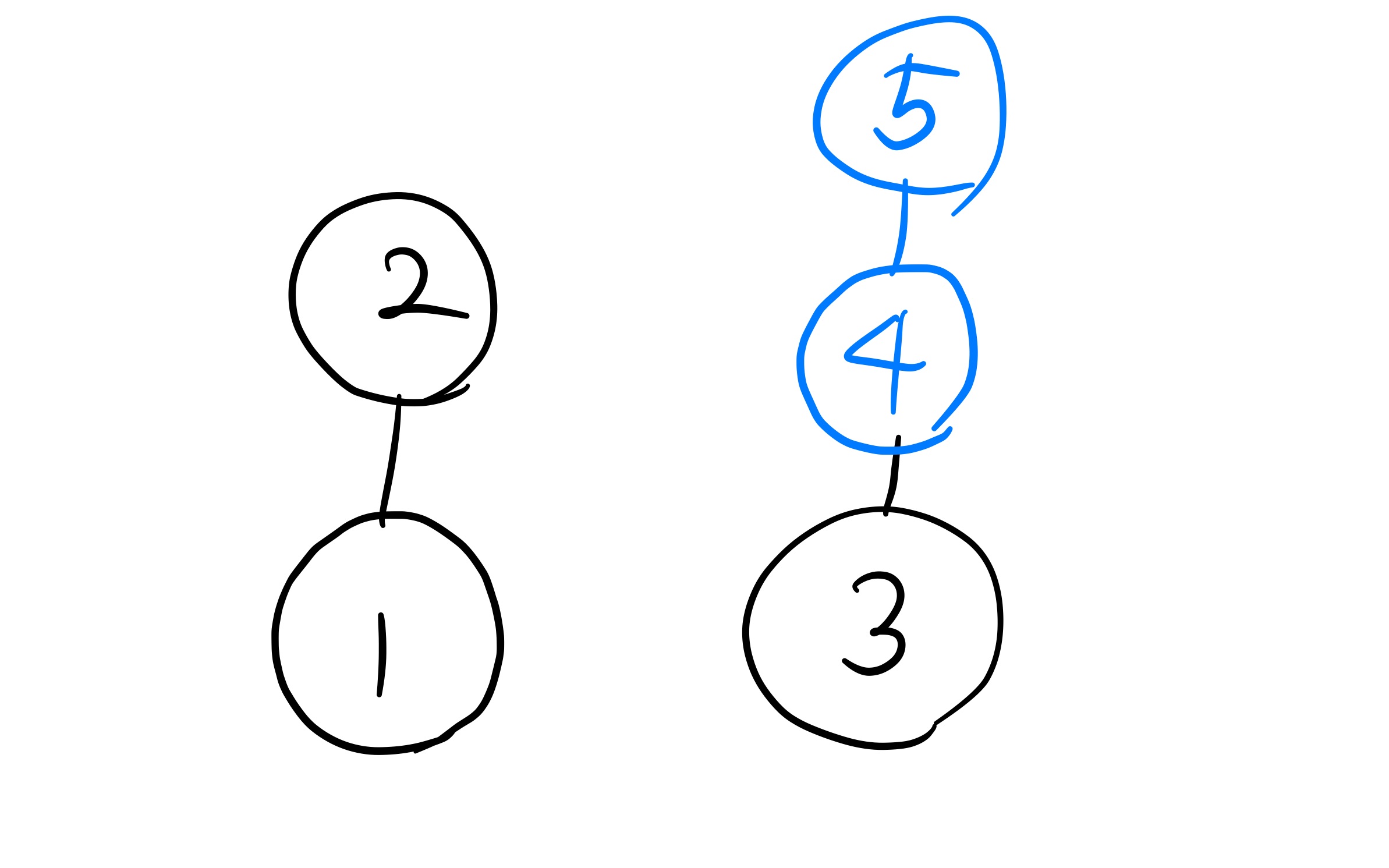
여기서 이제 네 번째 고객이 1번방을 요청했다. 그러면 우리가 바로 전에 한 것처럼 2번과 3번을 이어서 그려주면 된다.

여기서 알 수 있는 것은 이미 1,2,3,4 번 방이 다 차있으며, 1,2,3,4 번을 다음 고객이 요청할 경우 5번 방을 배정해야 한다는 것이다. 5번 방은 현재 그래프에서 루트 노드이다. 따라서 이미 Map에 들어있는 Key 값들에 대해서, 업데이트가 필요한 경우는 업데이트를 해 주어야 하고 그 결과는 다음과 같다.

이런 식으로 매번 방 배정을 할 때마다 새로운 key 값이면 Map에 (K,V) 쌍을 추가해 주고, 업데이트가 필요한 정보들은 적절하게 업데이트를 해 주면 된다. 그렇게 하면 그 이후에 새로운 방을 요청하는 고객이 나타났을 때 바로 비어있는 방을 배정할 수가 있다. 유니온 파인드 알고리즘에서 find() 메서드에 해당되는 부분은 아래 코드에서 line 13 ~ 22 부분에 구현했다.
이런 방법으로 코드를 작성하면 시간복잡도 O(N*logN) 으로 풀 수가 있으며, 제한 시간 내에 효율성까지 통과할 수가 있게 된다.

내가 제출한 자바 소스코드이다.
유니온 파인드는 자주 나오는 유형은 아니지만, 해당 유형의 문제가 나왔을 때 이 문제가 유니온 파인드로 풀 수 있는지를 파악하면 어렵지 않게 풀 수 있다는 생각이 들었다. 직접 구현하면서 연습해 보자!