백준 1300 / 이분 탐색 (Binary Search) / JAVA
오늘은 백준 1300번 <K번째 수> 문제를 풀어 보려고 한다.
https://www.acmicpc.net/problem/1300
이 문제는 이분 탐색을 사용하여 푸는 문제이다. 이분 탐색을 알고, 약간의 아이디어만 생각해 낼 수 있으면 풀 수 있는 무난한 난이도의 문제인 것으로 보인다.
이분 탐색은 정렬이 되어 있는 데이터에 대해서 순차적으로 값을 찾는 방법이 아닌 탐색 범위를 절반씩 줄여 나가면서 찾아가는 탐색 알고리즘이다. 해당 범위의 중앙 값을 찾고 찾는 값과 비교하여, 찾는 값보다 중앙 값이 크면 두 범위 중 작은 범위에서 탐색을 이어나가고, 찾는 값보다 중앙 값이 작으면 반대로 큰 범위에서 탐색을 이어 나가는 방법이다.
순차 탐색은 최악의 경우 시간복잡도가 O(N)까지 나타난다. N = 1,000,000,000 인 경우 최악의 상황에서 10억 번을 탐색해야 한다는 것이다. 하지만 이분 탐색은 탐색 범위를 절반씩 줄여 나가기 때문에 시간복잡도는 O(logN) 으로 나타난다. N = 10억 이어도, 30번 정도면 탐색을 할 수 있다는 의미이다. N이 커지면 커질수록 시간을 급격하게 절약할 수 있는 방법으로 반드시 알고 가야 한다.

그러면 이분탐색을 이해했으니 이 문제를 본격적으로 풀어보자.
2차원 배열 A는 N X N 형태로 N은 10^5 이하 이다. 그리고 A[i][j] = i*j 의 값이 들어가 있고 A 배열에 들어있는 모든 값들, 다 합치면 N^2 개가 될 텐데, 이 값들은 1차원 배열 B에 오름차순으로 들어있다. 이 때 B[k]를 구하는 것으로, k는 10^9 이하이다. 따라서 이 문제는 순차적인 탐색으로 풀면 시간초과로 틀리게 된다.
그래서 이 문제는 이분 탐색을 사용해야 한다. 인덱스의 최솟값인 1부터 최댓값인 K를 각각 min, max 값으로 초기에 설정하고 이분 탐색을 진행한다. 그리고 이 문제에서 사용한 아이디어는 다음과 같다.
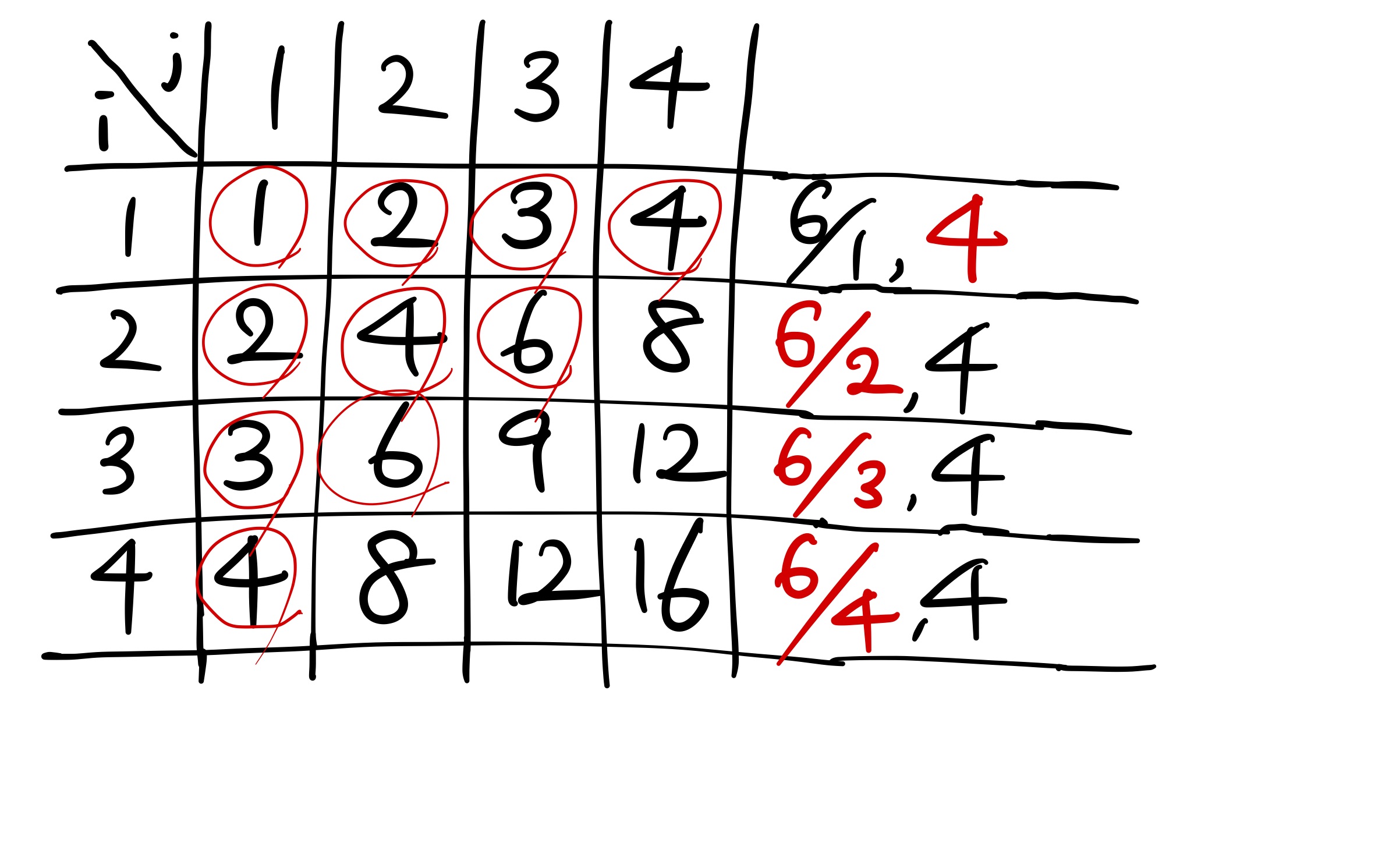
예를 들어 A가 4X4 배열이라고 한다면 다음과 같이 배열에 값들이 들어갈 것이다.

여기에서 만약 B[10]을 구한다고 하면 B 배열에서 10번째까지 오름차순으로 계산되는 원소들은 아래처럼 나타난다. 그리고 우리가 구하는 값은 6일 것이다.

우리가 구하려는 이 값이 S라고 했을 때 이 S는 1행부터 N행까지 i번째 행에서 min(S/i, N)을 더한 값이라는 것을 알 수가 있다.
따라서 우리는 1부터 K 사이에 있는 S값을 찾아야 하고, 이 과정에서 이분탐색을 사용하여 문제를 풀 수가 있다. 만약에 어떤 S에 대해서 1행부터 N행까지 i번째 행에서 min(S/i, N)을 더한 값이 K보다 작으면 S값을 더 큰 범위에서 찾아야 한다는 의미이고, K보다 크면 S값 이하에서 문제에서 구하려는 답이 있다는 의미이므로 S값을 우선 적어두고 더 작은 범위에서 탐색을 계속해 나아가야 한다.
이분탐색으로 풀 경우 이 문제의 시간 복잡도는 O(NlogN)으로 계산해 볼 수가 있다.

내가 푼 자바 소스 코드는 다음과 같다.