백준 10422 / 동적 계획법 (Dynamic Programming) / JAVA
오늘 설명할 문제는 백준 10422번 <괄호> 문제이다.
https://www.acmicpc.net/problem/10422
10422번: 괄호
‘(‘, ‘)’ 문자로만 이루어진 문자열을 괄호 문자열이라 한다. 올바른 괄호 문자열이란 다음과 같이 정의된다. ()는 올바른 괄호 문자열이다. S가 올바른 괄호 문자열이라면, (S)도 올바른 괄호 문자열이다. S와 T가 올바른 괄호 문자열이라면, 두 문자열을 이어 붙인 ST도 올바른 괄호 문자열이다. (()())()은 올바른 괄호 문자열이지만 (()은 올바른 괄호 문자열이 아니다. 괄호 문자열이 주어졌을 때 올바른 괄호 문자열인지 확인하는 방법은 여러
www.acmicpc.net
이 문제는 동적 프로그래밍을 사용해서 푸는 문제이다. 아이디어를 알고 나면 되게 쉽지만, 아이디어를 생각하는 것이 조금 어려울 수도 있을 것 같다. 필자의 경우 여러 차례 삽질을 하고 틀리고 나서 맞힌 문제이다.
먼저 동적 계획법(Dynamic Programming, 이하 DP)에 대해서 간단하게 설명해 보려고 한다.
우리가 크고 복잡한 문제를 풀려고 할 때 한 번에 그 문제를 해결하려면 방법이 보이지 않는 경우가 많다. 하지만, 작은 문제들로 나누어서 생각하면 답을 찾을 수 있는 경우가 있다. 이와 같이 큰 문제를 작은 문제로 나누어서 푸는 방법 중에서, 작은 부분 문제들이 반복해서 사용되는 경우를 우리는 DP라고 한다. 만약에 작은 문제가 반복되지 않으면, 그 경우는 분할 정복(Divide and Conquer)이라고 한다.
DP에서는 작은 문제를 한 번씩만 푼다. 그렇게 함으로써 그냥 풀면 작은 문제를 여러 번 풀어야 하는데, 그에 비해 시간을 많이 단축시킬 수 있다. 작은 문제를 한 번만 풀기 위해서는 작은 문제를 어딘가에 메모해 놓아야 한다. 이와 같이 작은 문제를 메모해 놓고 사용하는 방법을 메모이제이션(Memoization)이라고 한다.
예를 들어 피보나치 수열을 살펴보도록 하자. 피보나치 수열은 1,1,2,3,5,8,13,... 이와 같이 어떤 숫자가 그 전과 그 전전 숫자의 합으로 이루어진 수열을 말한다. 여기에서 만약에 7번째 숫자를 구하려면 얼마나 연산을 해야 할까?
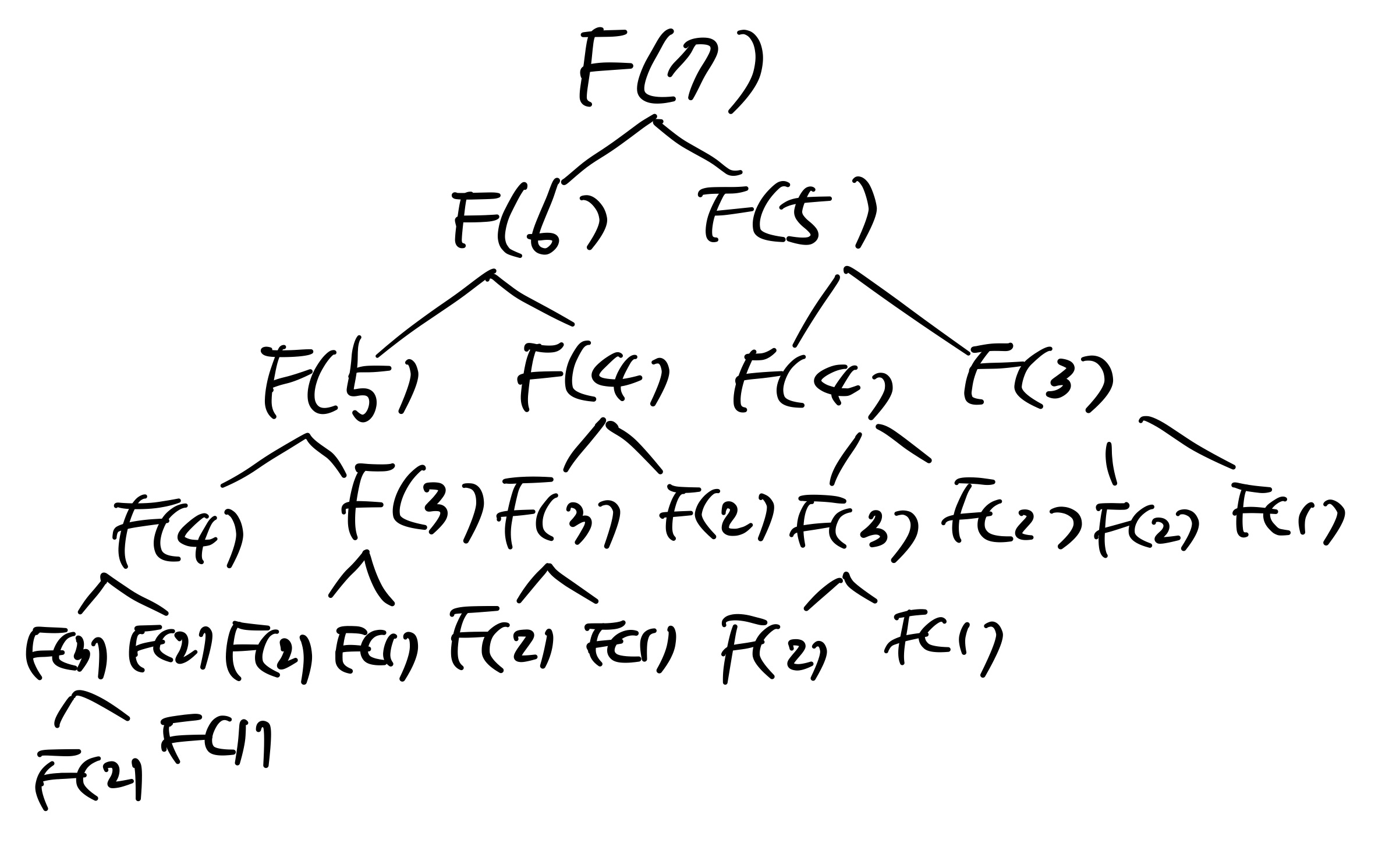
무려 12번을 해야 한다. F(7) = F(6) + F(5) = ( F(5) + F(4) ) + F(5) = ... 이런 식으로 말이다. 숫자가 커지면 이 연산을 기하급수적으로 많이 해야 한다.
하지만 우리가 매번 피보나치 수열을 구할 때마다 그 값을 배열에 메모해 놓으면 그 배열의 값을 참조해서 한 번에 연산을 할 수가 있다.
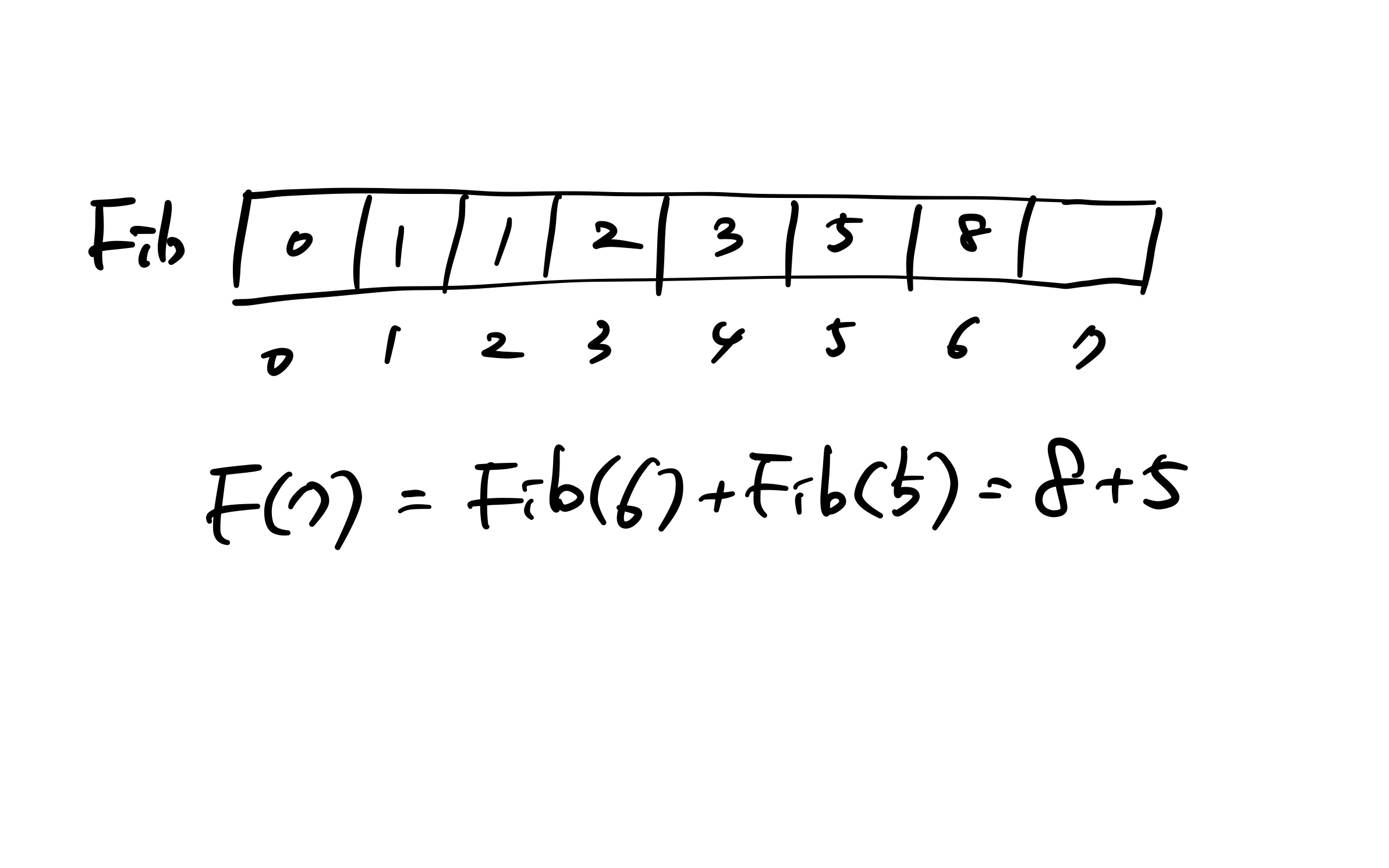
DP는 구현하는 방식이 Bottom-up과 Top-down 방식 두 가지가 있다. Buttom-up은 작은 문제부터 차근차근 구해서 정답을 찾는 과정이고, Top-down은 큰 문제를 잘게 쪼개면서 문제를 푸는 방식이다. 재귀함수가 대표적인 Top-down 방식이다. 두 방식 중에 절대적으로 좋은 방식은 없으며 문제에 맞게 적절한 방식을 사용해서 풀어주면 된다.
그러면 지금부터 <괄호> 문제를 DP로 풀어 보도록 하자.
먼저 이 문제에서 길이 N인 올바른 괄호 문자열 갯수에 대한 메모를 해 놓을 int형 배열 dp를 하나 설정한다. 당연히 dp는 인덱스가 홀수일 경우 올바른 괄호 문자열을 만들 수 없으므로 0이다.
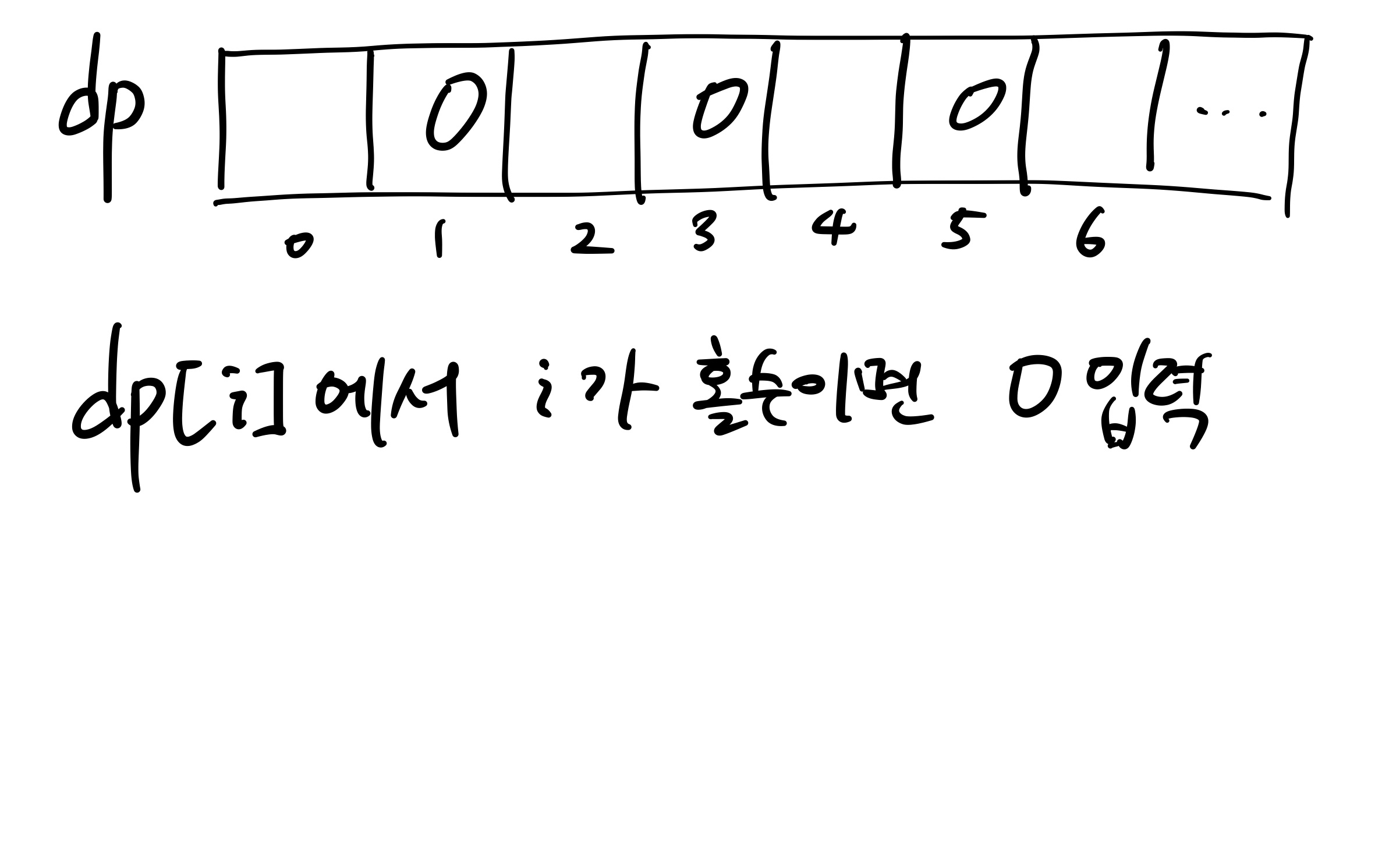
i가 0이고 2인 경우는 하나씩 밖에 없음을 알기 때문에 초기에 각각 1을 대입해 준다.
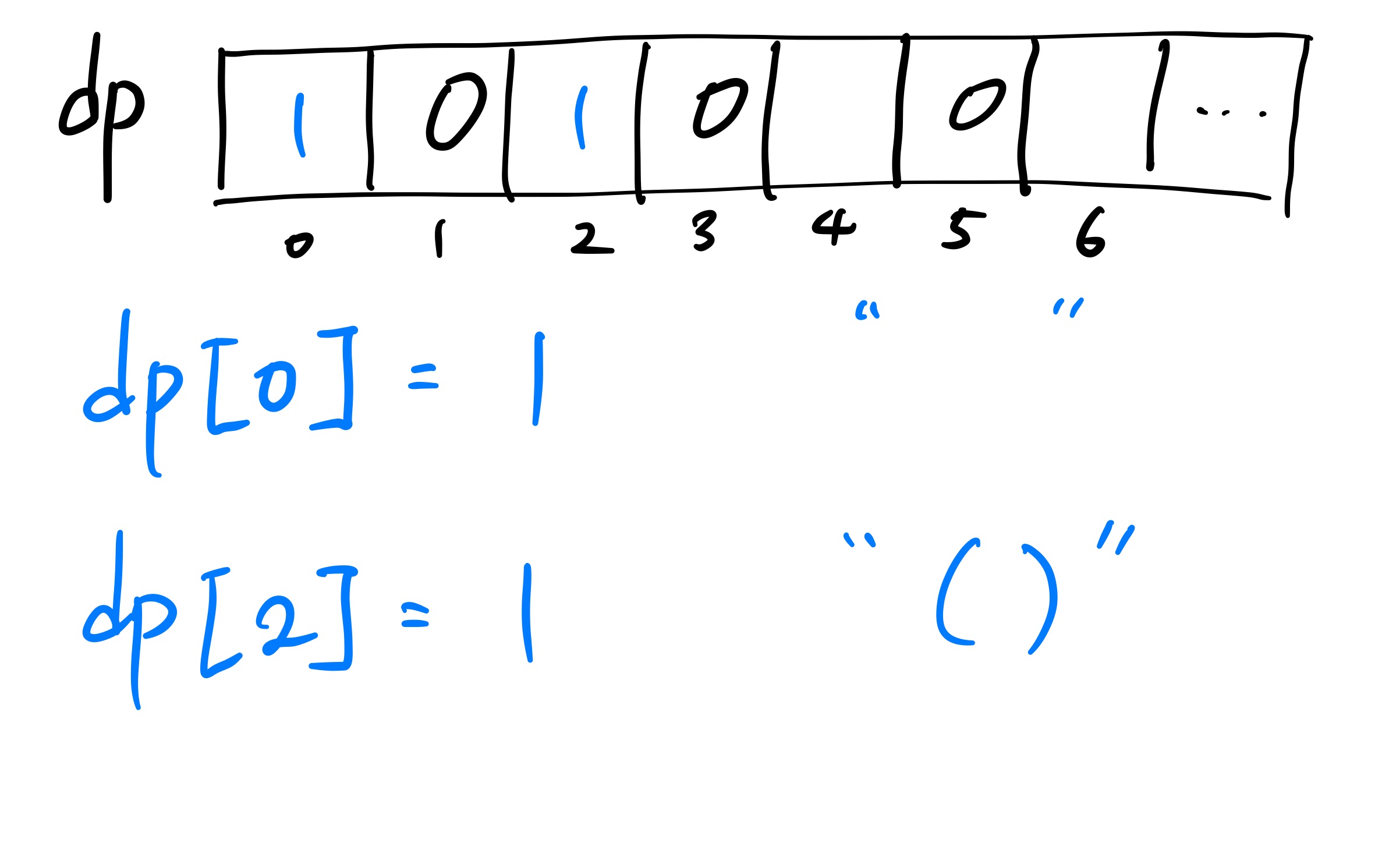
이제는 i = 4인 경우를 확인해 볼 차례이다. 갯수가 많지 않으므로 직접 세어 보면 2개가 나옴을 쉽게 알 수 있다.
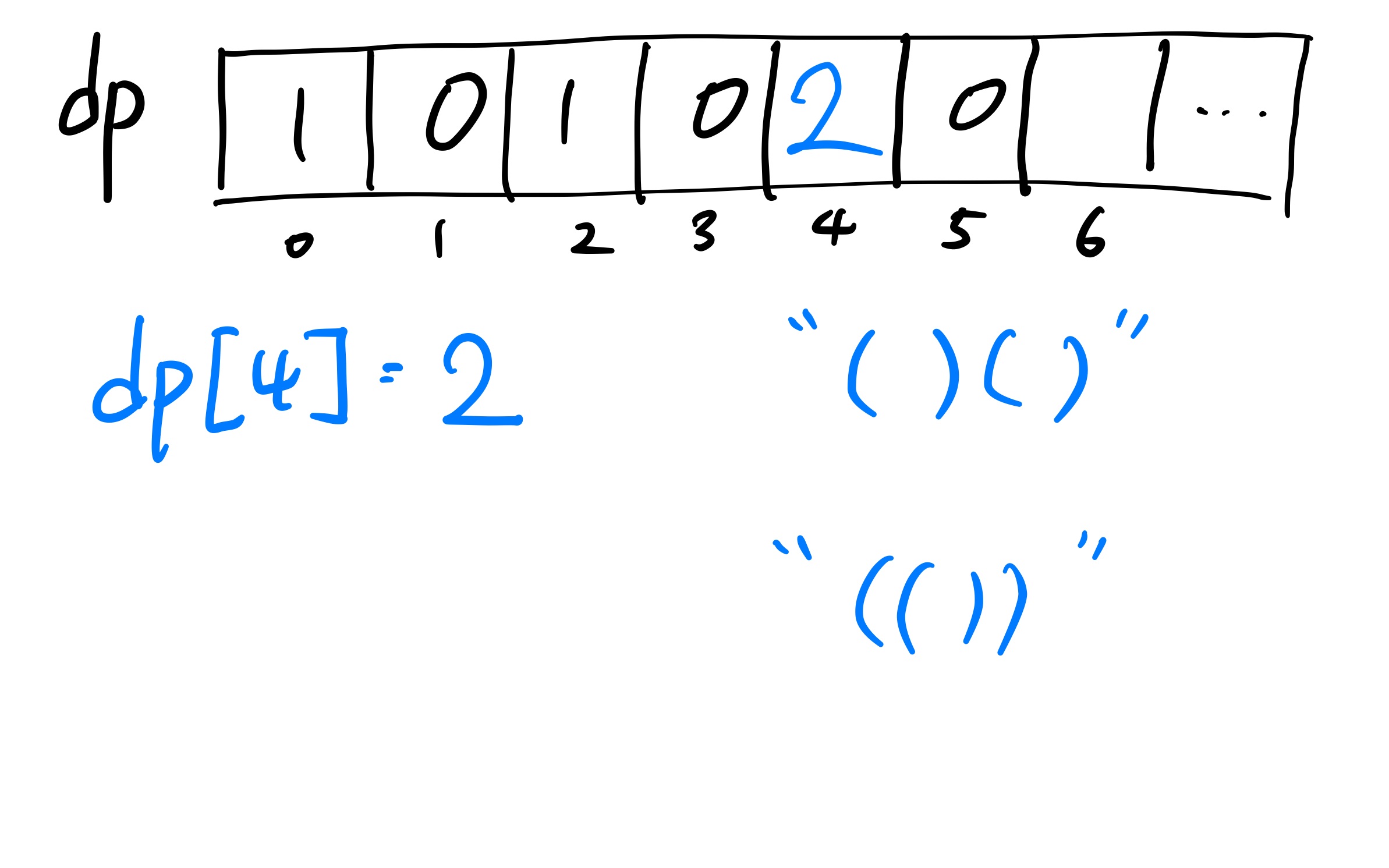
여기에서 점화식을 생각해 보아야 하는데, 이 부분이 조금 생각하기 까다로울 수 있다. 아래와 같은 규칙으로 점화식을 구해볼 수 있는데 이렇게 계산을 하면 중복이 발생하지 않고 전체 문자열의 갯수를 셀 수 있다.
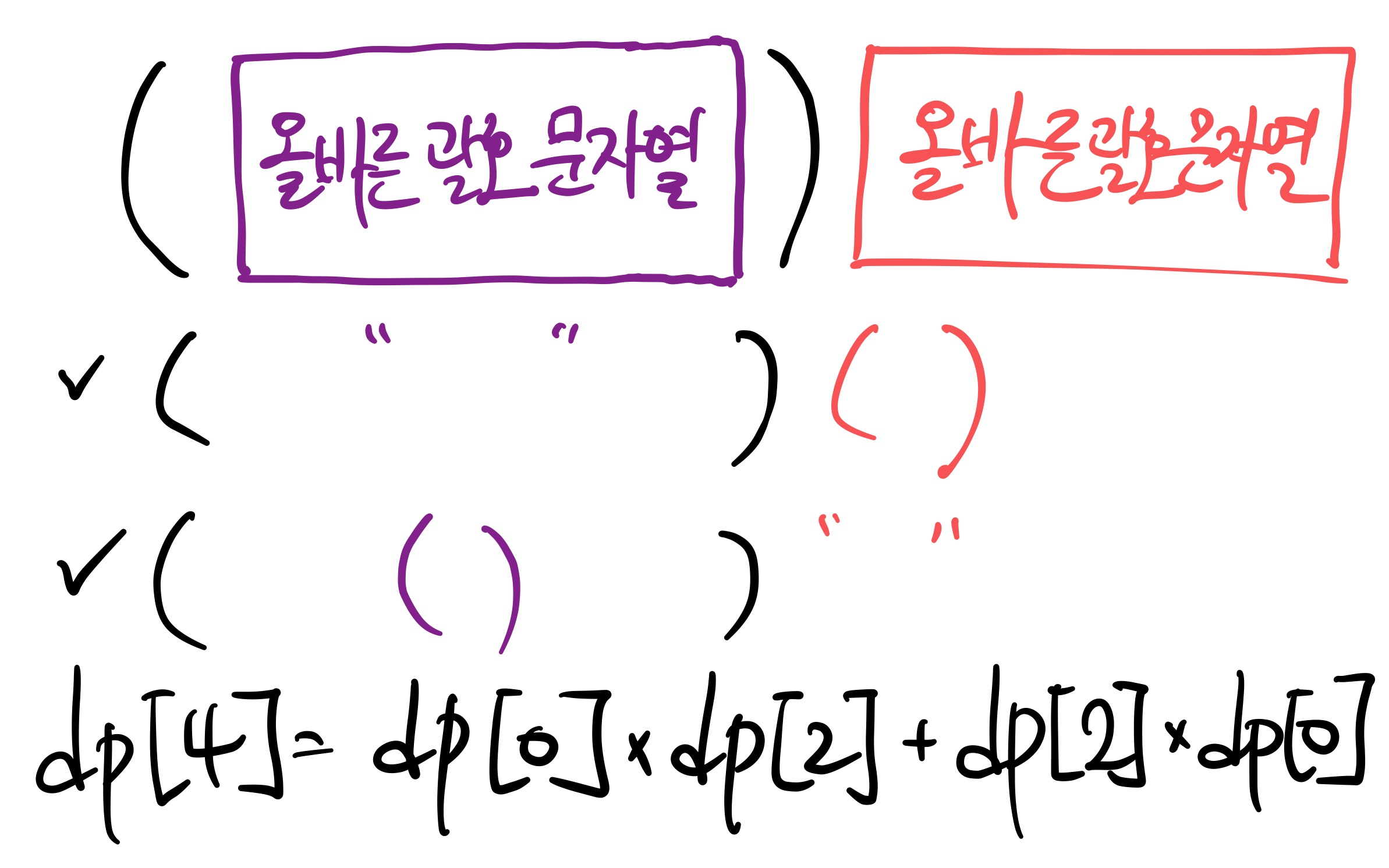
그렇다면 이번에 이 점화식을 i = 6 인 경우에 한 번 적용을 해 보도록 하자.
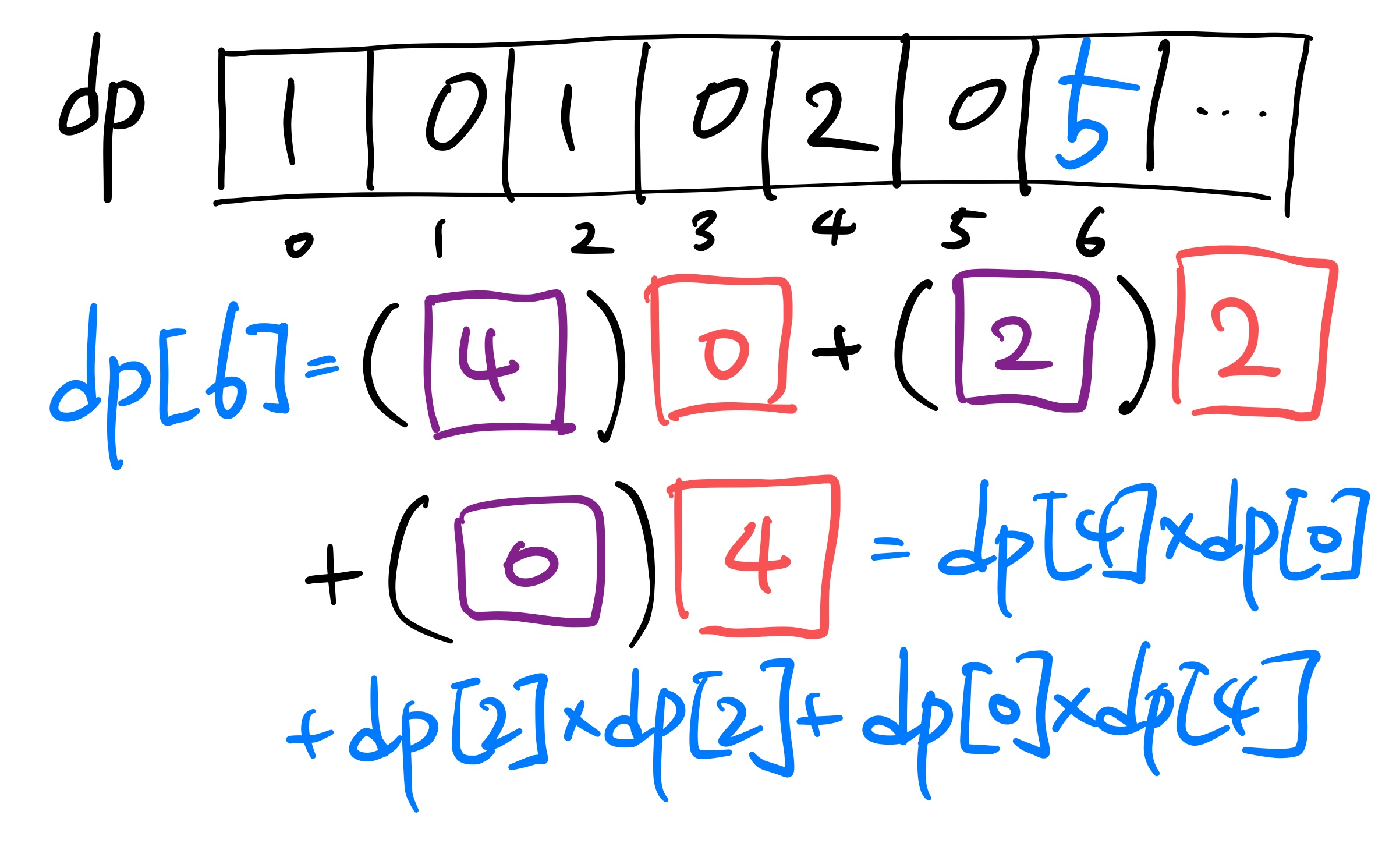
실제로 i = 6 인 경우에 아래와 같은 올바른 괄호 문자열이 나오게 되고, 점화식이 올바르게 작성되었다는 것을 알 수 있다.
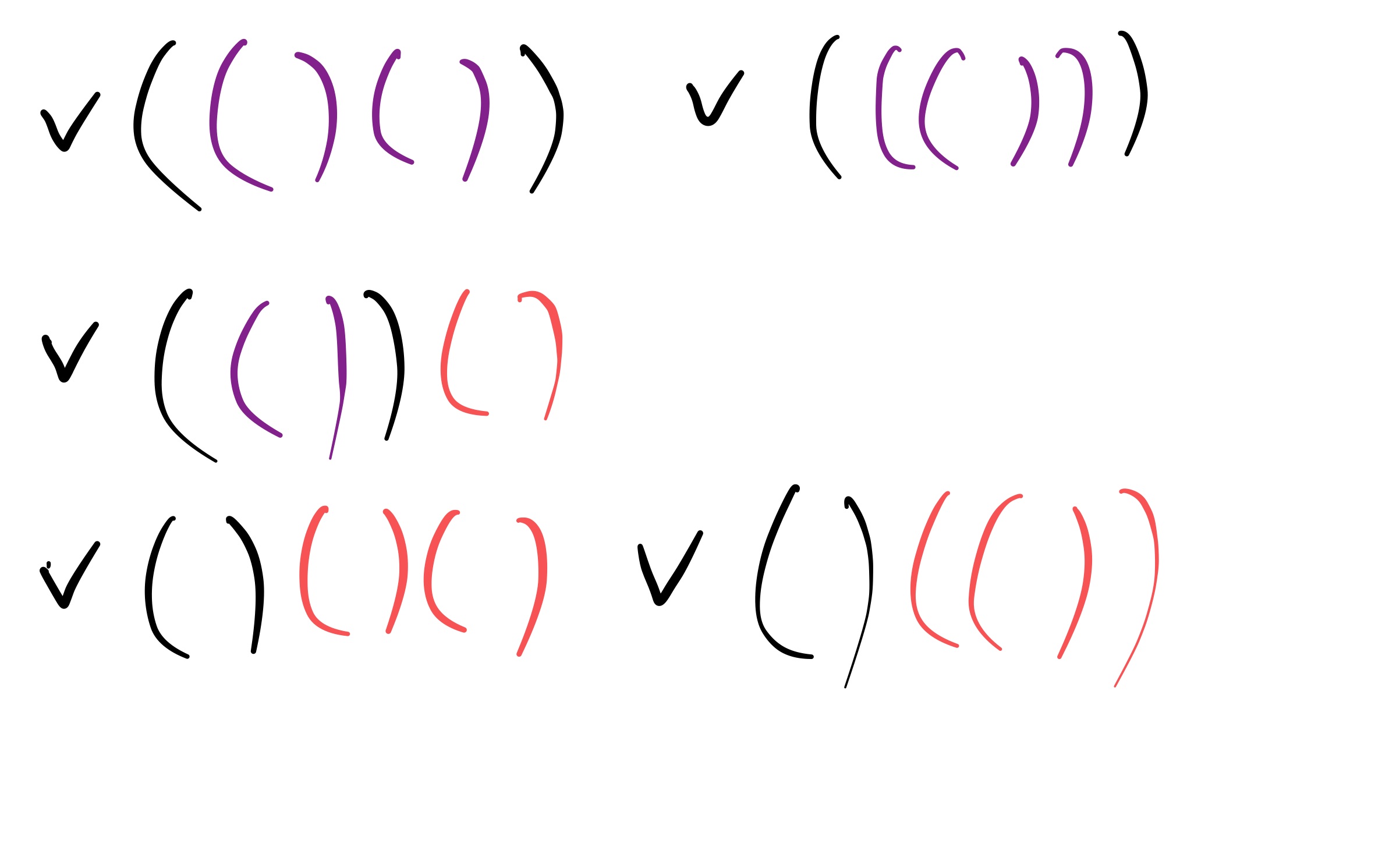
따라서 길이가 N인 dp를 채워 줄 코드는 아래처럼 작성을 해 볼 수 있다. 문제에서 길이 L이 최대 5000이라고 하였으므로 실제 코드에서는 N = 5000을 넣어서 작성했다. 그리고 문제에서 배열에 해당 갯수를 1,000,000,007로 나누어준 값을 입력하라고 하였으므로 매 번 반복할 때 마다 나누기를 해준다.

이렇게 이중 for문을 돌리면 O(N^2)의 시간복잡도를 가지고 0부터 N까지의 모든 길이에 따라 올바른 괄호 문자열의 갯수를 바로 찾아줄 수 있는 dp 배열이 완성된다.

내가 제출한 자바 소스 코드는 아래와 같다.
점화식을 구현하는 부분이 생각하기 조금 쉽지 않았다. 이 문제 역시 DP를 연습해 보기 좋은 문제이다. 꼭 풀어보기를 추천한다!