백준 1865 / 벨만 포드 알고리즘(Bellman Ford) / JAVA
오늘은 백준 1865번 웜홀 문제를 풀어보려고 한다.
https://www.acmicpc.net/problem/1865
1865번: 웜홀
문제 때는 2020년, 백준이는 월드나라의 한 국민이다. 월드나라에는 N개의 지점이 있고 N개의 지점 사이에는 M개의 도로와 W개의 웜홀이 있다. (단 도로는 방향이 없으며 웜홀은 방향이 있다.) 웜홀은 시작 위치에서 도착 위치로 가는 하나의 경로인데, 특이하게도 도착을 하게 되면 시작을 하였을 때보다 시간이 뒤로 가게 된다. 웜홀 내에서는 시계가 거꾸로 간다고 생각하여도 좋다. 시간 여행을 매우 좋아하는 백준이는 한 가지 궁금증에 빠졌다. 한 지점에서
www.acmicpc.net
이 문제는 개인적으로 정말 많이 틀리고 나서 해결했던 문제이다. 그래서 더욱 꼼꼼하게 문제를 푸는 과정을 살펴보려고 한다.
이 문제는 그래프 유형이며, 웜홀이라는 음수값을 가진 edge가 존재한다. 그래서 다익스트라 알고리즘을 쓸 수는 없고, 벨만-포드 알고리즘(Bellman-Ford Algorithm)을 사용해야 한다. 각각의 node에 도달하는 최단거리를 찾아준 후 negative cycle(한 바퀴를 돌았을 때 음수가 나오는 사이클)이 있는지를 체크해서 존재하지 않으면 "YES", 존재하면 "NO"를 출력해 주면 된다.
벨만 포드 알고리즘에 대해서 간단하게 설명하고 문제를 풀어보도록 하자. 음의 가중치를 가진 그래프에서 최단 경로를 찾을 때 사용하는 벨만포드 알고리즘은 기본 전제가 시작 노드 s에서 v까지 거리의 최단 경로는 s에서 u까지의 최단 경로에 u에서 v사이의 가중치를 더한 값이라는 것이다.
D(s, v) = D(s, u) + w(u, v)
그래서 모든 edge에 대해서 edge relocation을 수행해 주어야 한다. 따라서 s에서 u에 이르는 최단 경로를 찾기 위해서는 u를 제외한 전체 node의 갯수만큼(V - 1) edge relocation을 해 주어야 한다. 이 작업을 모든 edge에서 수행한다. node의 갯수가 V이면, 가능한 최대 edge의 갯수는 V(V - 1)/2 이므로 벨만-포드 알고리즘의 시간복잡도는 O(V * V(V - 1)) = O(V^3) 이다.

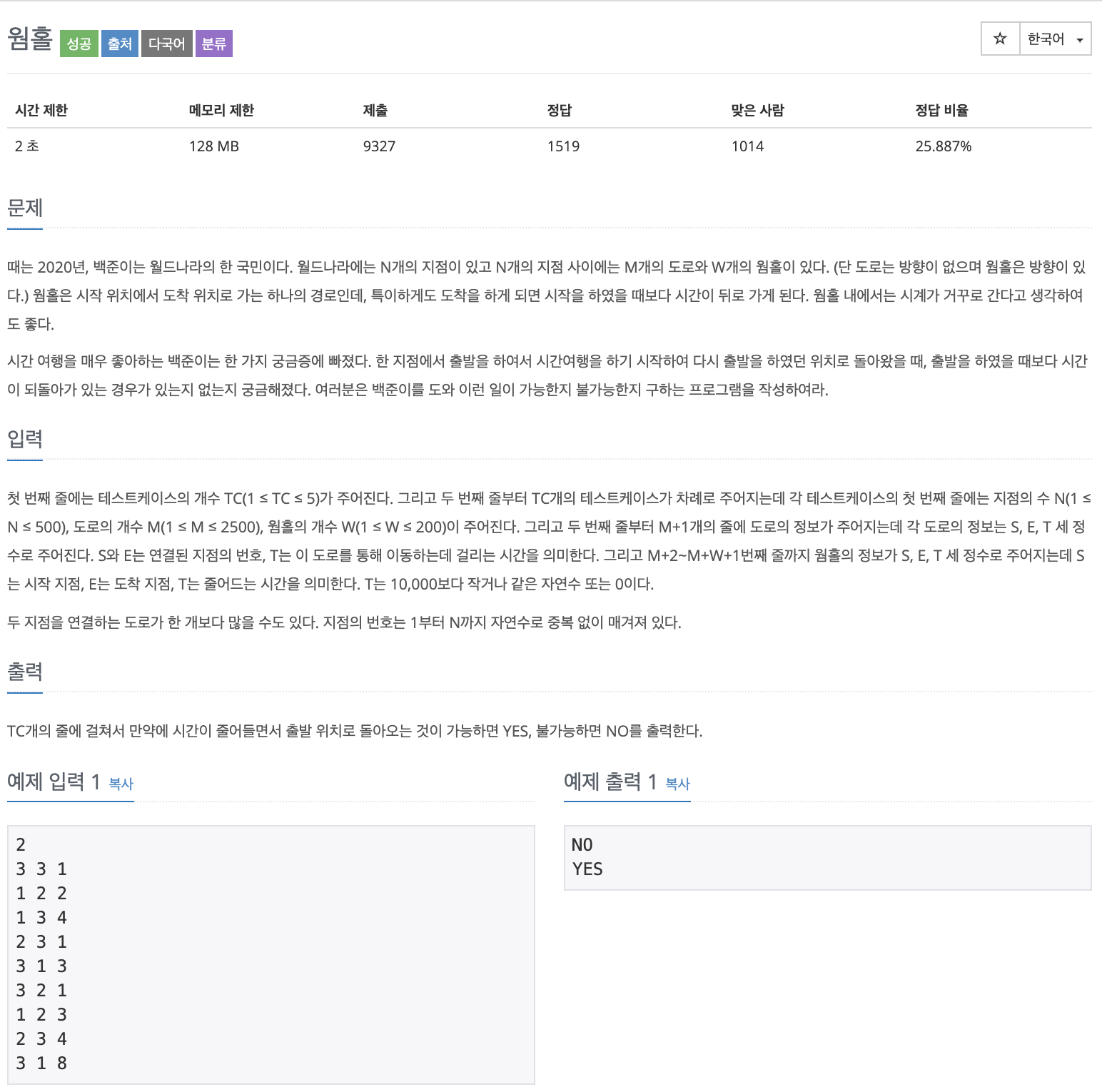
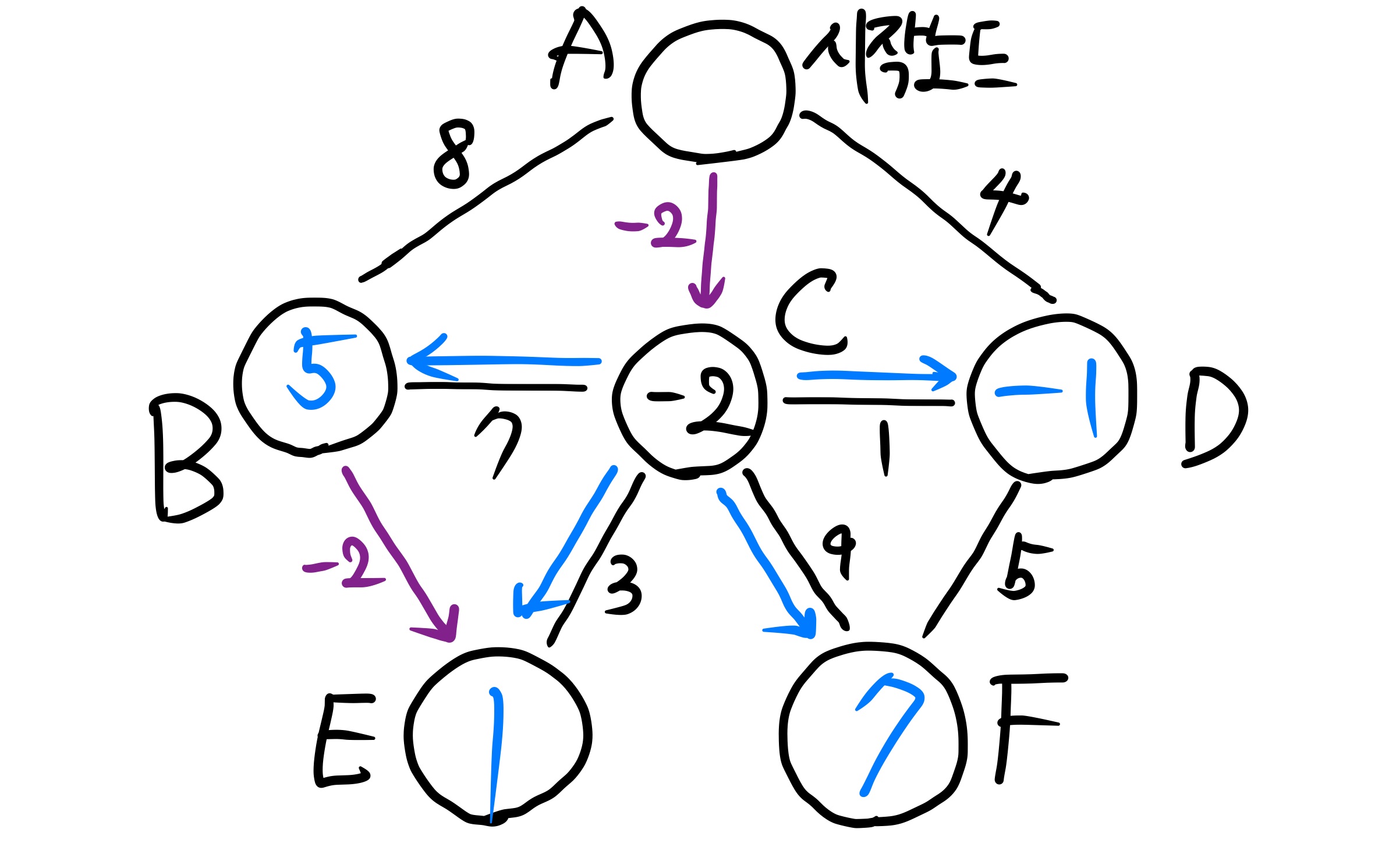
아래와 같은 그래프가 있다고 생각해 보자
검은색 양의 가중치를 가진 간선은 양방향이고, 보라색 음의 가중치를 가진 간선은 단방향이다. 이는 웜홀 문제에 맞게 설정하였다. 시작 노드를 A라고 하면, 나머지 (V - 1)개의 노드는 초기값을 INF(원래는 무한대를 의미하지만 여기선 굉장히 큰 정수값)로 잡는다.
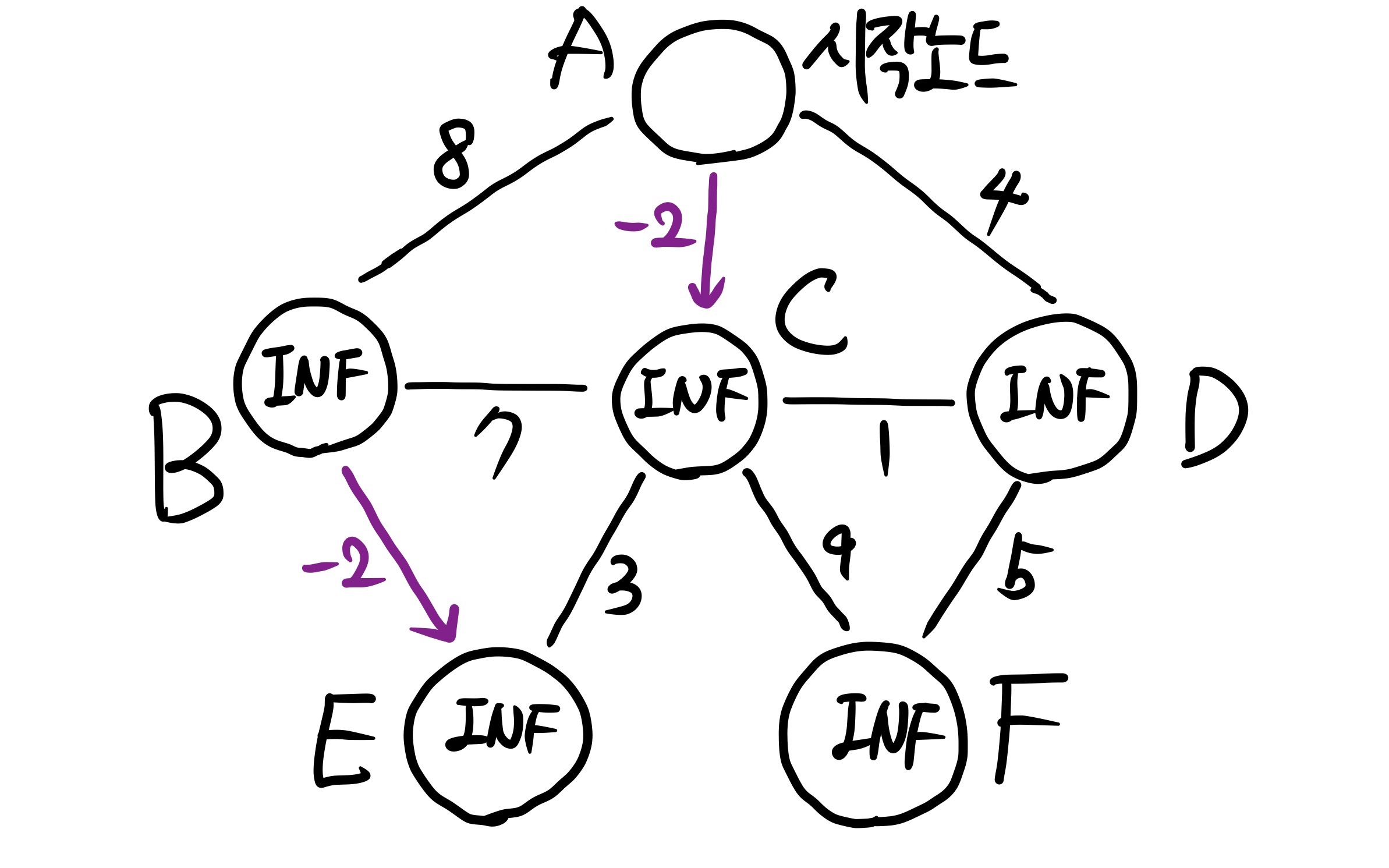
처음은 시작노드 A에서 edge relocation을 하는 것으로 시작한다. A에서 edge가 있는 모든 노드들에 대해 edge relocation을 수행하고 D(s, v) > D(s, u) + w(u, v) 이면 해당 노드의 값을 업데이트 해준다. 처음에는 u = s 이고 D(s, u) = D(s, s) = 0 이므로 모든 edge에 대해서 INF = D(s, v) > D(s, u) + w(u, v) = w(u, v) 가 만족되고, 모두 업데이트를 해 준다.
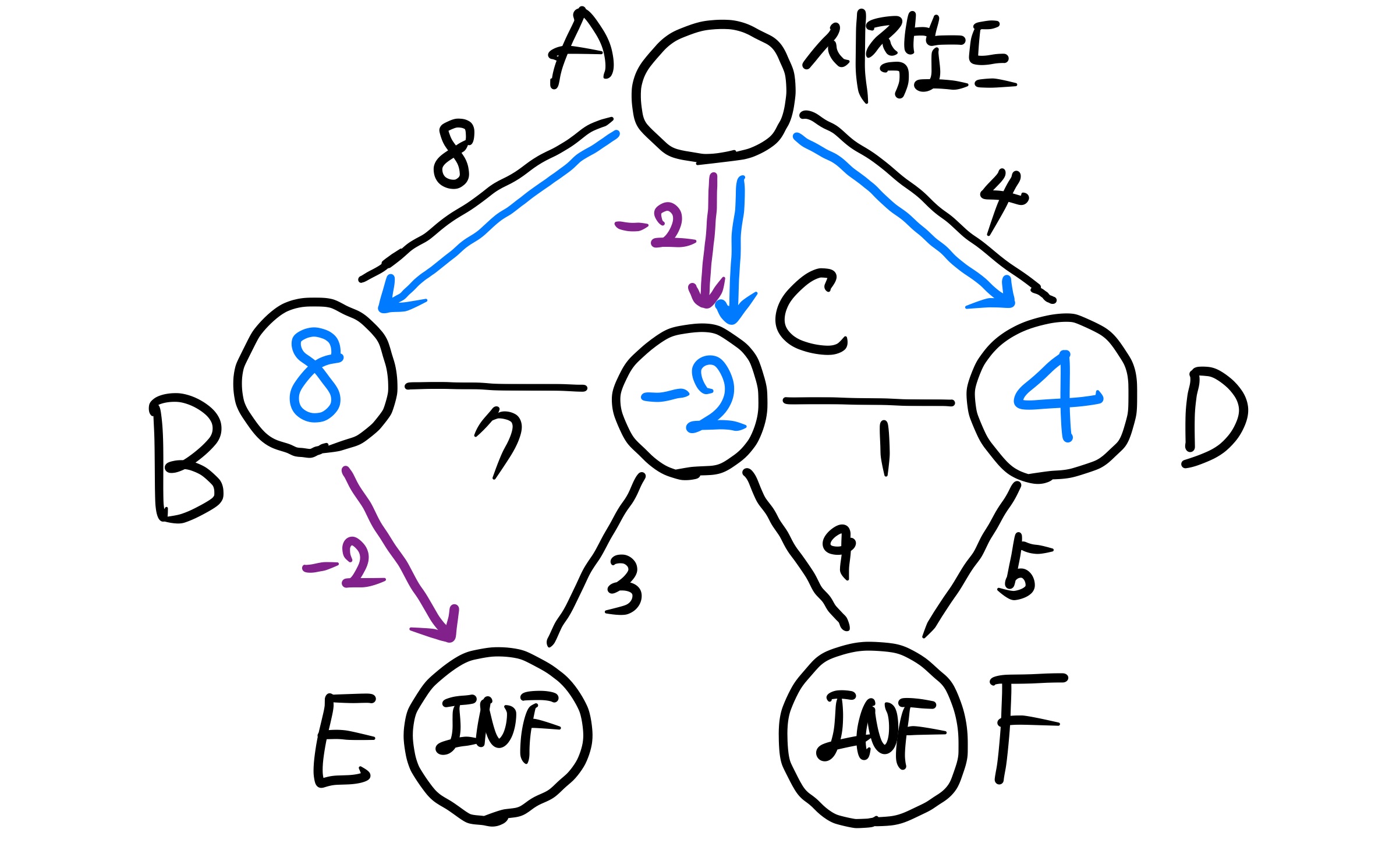
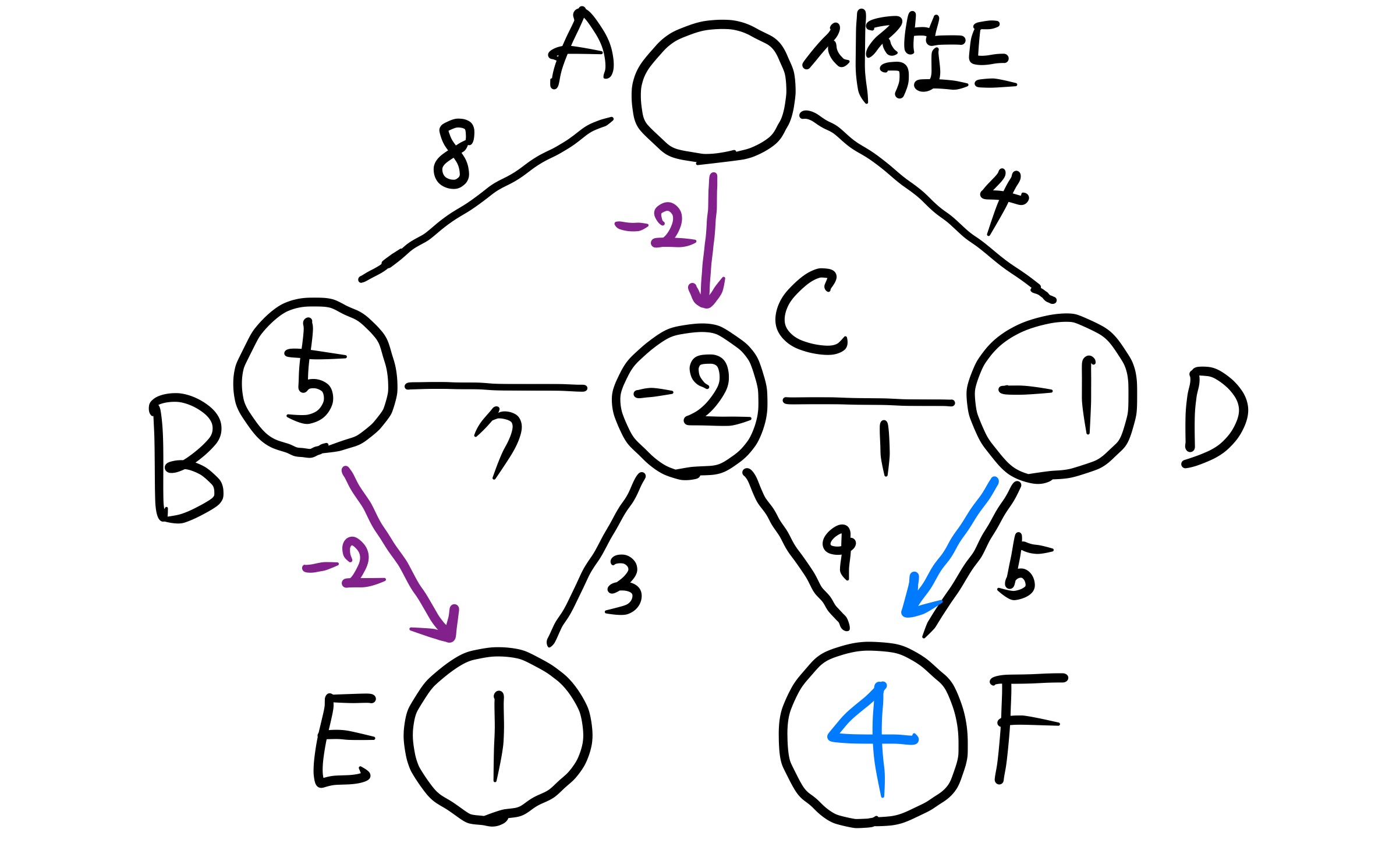
첫 번째 edge relocation이 끝났다. 이 번에는 B를 시작으로 두 번째 edge relocation을 시작한다. edge relocation은 (V - 1)번 실행하는데, 그 전에 Update가 더 이상 없는 것이 확인되면 중단할 수 있다. 이 문제에서는 V = 6 이므로 최대 5번까지 edge relocation을 실행한다. 만약 D(s, v) < D(s, u) + w(u, v) 이면 업데이트를 수행하지 않는다.
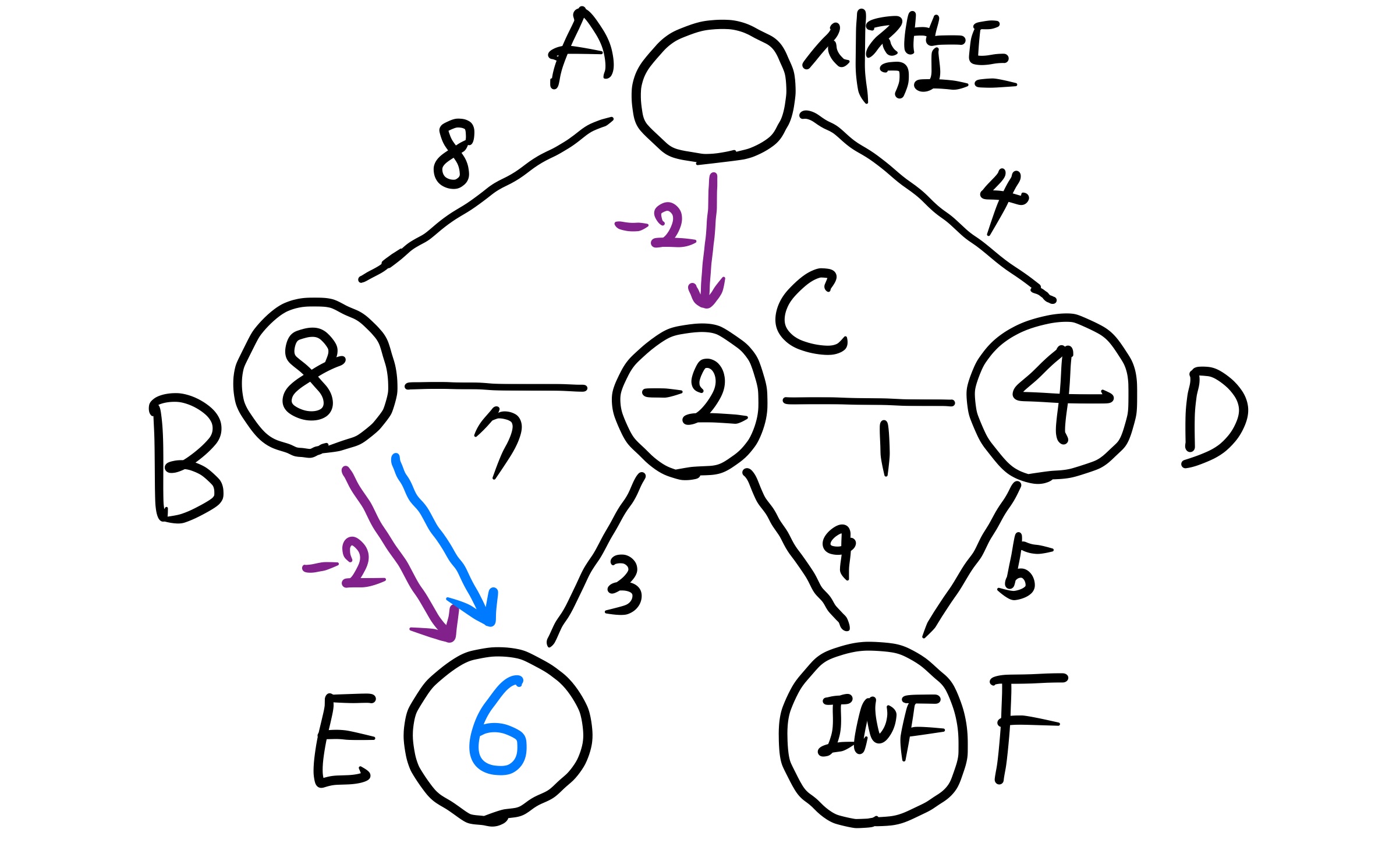
세 번째, 네 번째 edge relocation을 수행한다. 이 예제의 경우 네 번째 edge relocation에서 더이상 업데이트가 진행되지 않음을 확인했으므로 다섯번째 edge relocation은 진행하지 않는다.
따라서 최대 (V - 1)번의 edge relocation을 한 후 각각의 node에 이르는 최단 경로의 값은 다음과 같게 되었다.
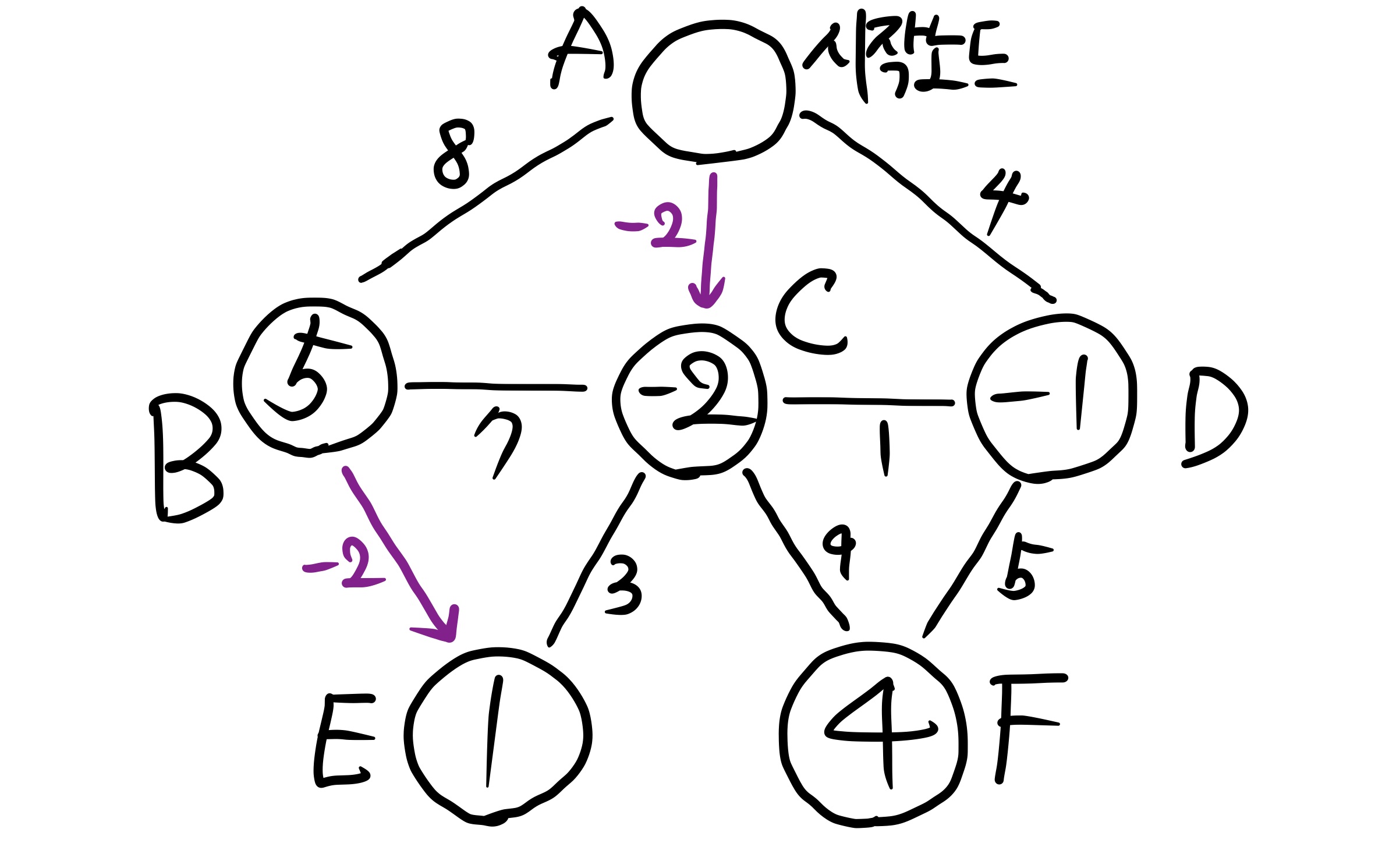
여기에서 끝난 것이 아니다. 벨만-포드 알고리즘은 음수 가중치가 있는 그래프에서 수행하기 때문에 때로는 무한하게 돌면 돌 수록 최단 경로가 작아지는 경우도 충분히 발생할 수 있다. 이런 경우를 negative cycle이라고 하는데, 돌면 돌수록 값이 계속 무한하게 업데이트 되기 때문에 이런 경우는 최단 경로를 구할 수 없다. 따라서, negative cycle 이 있는지 확인을 해 보아야 한다. 모든 edge에 대해서 수행 시 값이 업데이트 되는 경우가 있는지 체크한다. 이 때 한 번이라도 업데이트가 일어나면 false를 리턴한다. 위의 예제에서는 업데이트가 일어나지 않는다.

이제 벨만-포드 알고리즘에 대해서 알았으니 본격적으로 웜홀 문제를 풀어보자.
나는 다음 순서로 웜홀 문제를 풀었다.
- 간선의 시작점, 끝점, 가중치가 들어간 Edge 클래스를 만든 후 이 edge들을 ArrayList에 다 담았다.(웜홀 포함)
- 각각의 node들은 시작 지점(1이라고 가정)에서 최단 경로를 의미하며 INF로 초기화했다. 단, 시작지점의 값은 0으로 한다.
- isUpdated는 업데이트가 하나라도 일어나는지를 판단하는 boolean 값이다. false로 시작해서, 한 번의 edge relocaion에서 한 번이라도 update가 일어나면 true값으로 바뀌고 매 번 edge relocation이 진행될 때 마다 false로 초기화된다. 만약 어떤 edge relocation이 끝났는데 isUpdated = false 라면 그 때 업데이트가 일어나지 않았다는 의미이므로 edge relocation을 조기 종료 한다.
- negative cycle 체크는 N 번째 edge relocation에서 일어나도록 했다. (원래 edge relocation은 N-1 번까지 해야 맞는데, N-1 번째 이후에 계속 루프가 돈다는 의미는 계속해서 사이클을 돌 때 마다 업데이트가 되고 있다는 의미이다.) 이 때 만약 update가 일어나면 이 그래프는 negative cycle을 가지고 있는 그래프고 이 문제에서 "YES", 즉 시간이 줄어들며 출발점으로 돌아올 수 있다는 결과를 반환해야 한다. 그렇지 않은 경우는 "NO"를 반환한다.
많이 틀렸던 이유는, edge relocation을 돌 때 충분하게 모든 노드의 모든 간선에 대해서 체크를 해 주지 않았던 것으로 보인다. 정말 모든 노드의 모든 간선을 체크해 주지 못하면, 이 문제는 채점 과정에서 틀릴 수 있다.
시간 복잡도는 N개의 node에 대해 (2M+W) 만큼 edge를 체크하므로 O(N * M) 으로 볼 수 있다.

웜홀 문제에 대한 나의 자바 소스코드는 아래와 같다.
꼼꼼하게 모든 가능성을 체크하지 않으면 틀리기 쉬운 문제다. 겸손하게 연습하도록 하자 ㅎㅎ